题目内容
已知![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,点
的左、右顶点,点![]() 在椭圆
在椭圆![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,已知![]() 是椭圆
是椭圆![]() 上不同于顶点的两点,直线
上不同于顶点的两点,直线![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .① 求证:
.① 求证:![]() ;② 若弦
;② 若弦![]() 过椭圆的右焦点
过椭圆的右焦点![]() ,求直线
,求直线![]() 的方程.
的方程.
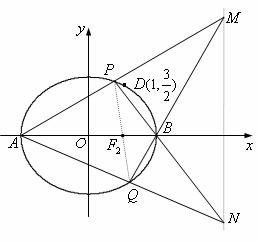
【命题意图】本题考查直线与椭圆的方程等相关知识,考查运算求解能力以及分析问题、解决问题的能力,较难题.
【答案】(Ⅰ)由题,![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上知
上知![]() ,则有:
,则有:
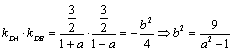 ,又
,又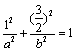 ,
,
以上两式可解得![]() ,
,![]() .所以椭圆
.所以椭圆![]() . ……4分
. ……4分
(Ⅱ)① 设![]() ,则直线
,则直线![]() :
:![]() 、直线
、直线![]() :
:![]() ,
,
两式联立消去![]() 得:
得:![]() ;
;
同理:直线![]() :
:![]() 、
、![]() :
:![]() ,联立得:
,联立得:![]() .……6分
.……6分
欲证:![]() ,只需证:
,只需证:![]() ,只需证:
,只需证:![]() ,
,
等价于:![]()
![]() ,
,
而![]() ,
,![]() ,所以
,所以![]() ,
,
故有:![]() . ……9分
. ……9分
② (ⅰ)当![]() 时,由
时,由![]() 可求得:
可求得:![]() ; …10分
; …10分
(ⅱ)当直线![]() 斜率存在时,设
斜率存在时,设![]() :
:![]() ,
,
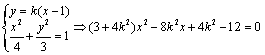
由(Ⅱ)知:![]() ,
,
将![]() ,
,![]() 代入上式得:
代入上式得:![]() ,
,
解得![]() ,由①知
,由①知![]() .
.
综合(ⅰ) (ⅱ),![]() ,故直线
,故直线![]() :
:![]() . …
. …

练习册系列答案
相关题目
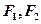 分别是椭圆
分别是椭圆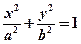
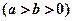 的左、右 焦点,已知点
的左、右 焦点,已知点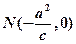 满足
满足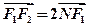 ,且
,且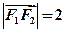 。设
。设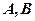 是上半椭圆上且满足
是上半椭圆上且满足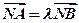 的两点。
的两点。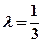 ,求直线AB的斜率。
,求直线AB的斜率。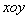
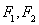
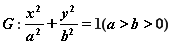
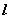
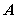
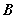
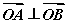
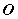
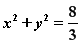
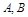 分别是椭圆
分别是椭圆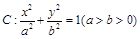 的左、右顶点,点
的左、右顶点,点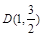 在椭圆
在椭圆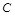 上,且直线
上,且直线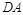 与直线
与直线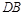 的斜率之积为
的斜率之积为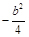 .
.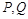 是椭圆
是椭圆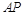 与
与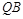 交于点
交于点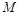 ,直线
,直线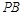 与
与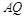 交于点
交于点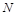 .①
求证:
.①
求证: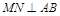 ;② 若弦
;② 若弦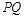 过椭圆的右焦点
过椭圆的右焦点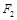 ,求直线
,求直线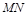 的方程.
的方程.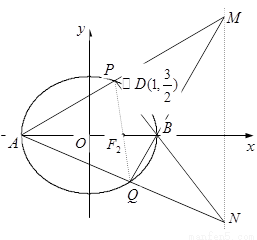
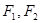 分别是椭圆
分别是椭圆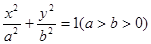 的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足
的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足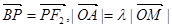 ,则实数
,则实数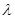 的取值范围为
。
的取值范围为
。 分别是椭圆
分别是椭圆
 的左、右
焦点,已知点
的左、右
焦点,已知点 满足
满足 ,且
,且 。设
。设 是上半椭圆上且满足
是上半椭圆上且满足 的两点。
的两点。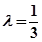 ,求直线AB的斜率。
,求直线AB的斜率。