题目内容
设
(Ⅰ)当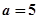 ,解不等式
,解不等式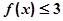 ;
;
(Ⅱ)当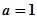 时,若
时,若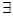
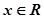 ,使得不等式
,使得不等式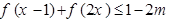 成立,求实数
成立,求实数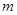 的取值范围.
的取值范围.

(Ⅰ)当
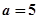 ,解不等式
,解不等式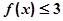 ;
;(Ⅱ)当
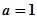 时,若
时,若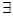
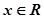 ,使得不等式
,使得不等式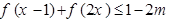 成立,求实数
成立,求实数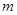 的取值范围.
的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:本题考查绝对值不等式的解法和不等式恒成立问题,考查转化思想和分类讨论思想.第一问,先将
 代入,解绝对值不等式;第二问,先将
代入,解绝对值不等式;第二问,先将 代入,得出
代入,得出 解析式,将已知条件转化为求最小值问题,将
解析式,将已知条件转化为求最小值问题,将 去绝对值转化为分段函数,通过函数图像,求出最小值,所以
去绝对值转化为分段函数,通过函数图像,求出最小值,所以 ,再解不等式即可.
,再解不等式即可.试题解析:(I)
 时原不等式等价于
时原不等式等价于 即
即 ,
,所以解集为
 . 5分
. 5分(II)当
 时,
时, ,令
,令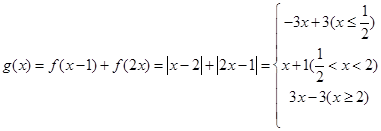 ,
,由图像知:当
 时,
时,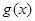 取得最小值
取得最小值 ,由题意知:
,由题意知: ,
,所以实数
 的取值范围为
的取值范围为 . 10分
. 10分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 ,若
,若 ,则
,则 _______
_______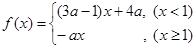 在
在 上是减函数,则
上是减函数,则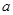 的取值范围是( )
的取值范围是( )
 ]
]
 ]
]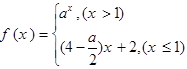 是R上的单调递增函数,则实数
是R上的单调递增函数,则实数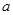 的取值范围为 ( )
的取值范围为 ( )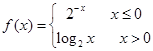 ,则
,则
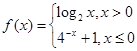 ,则
,则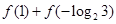 的值为 .
的值为 .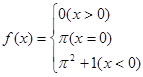 ,则
,则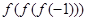 的值等于( )
的值等于( )


 ,则
,则 = .
= . ,那么
,那么 .
.