题目内容
(14分)设条件p:(4x-3)2-1≤0;条件q:x2-(2m+1)x+m(m+1)≤0,若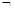 p是
p是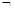 q的必要不充分条件,求实数m的取值范围.
q的必要不充分条件,求实数m的取值范围.
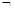 p是
p是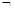 q的必要不充分条件,求实数m的取值范围.
q的必要不充分条件,求实数m的取值范围.解:设A={x|(4x-3)2-1≤0},B={x|x2-(2m+1)x+m(m+1)≤0},
故A={x|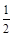 ≤x≤1},B={x|m≤x≤m+1}.
≤x≤1},B={x|m≤x≤m+1}.
由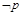 是
是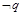 的必要不充分条件,从而p是q的充分不必要条件,即A
的必要不充分条件,从而p是q的充分不必要条件,即A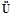 B,
B,
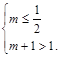 或
或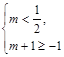 故所求实数a的取值范围是[0,
故所求实数a的取值范围是[0,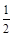 ].
].
故A={x|
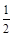 ≤x≤1},B={x|m≤x≤m+1}.
≤x≤1},B={x|m≤x≤m+1}.由
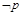 是
是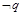 的必要不充分条件,从而p是q的充分不必要条件,即A
的必要不充分条件,从而p是q的充分不必要条件,即A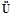 B,
B,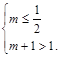 或
或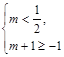 故所求实数a的取值范围是[0,
故所求实数a的取值范围是[0,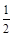 ].
].略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
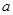 >1”的
>1”的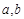 是实数,则“
是实数,则“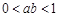 ”是“
”是“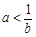 ”或“
”或“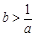 ”的…………( )
”的…………( ) 是
是 的.
的.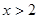 ”是“
”是“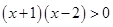 ”的( )
”的( )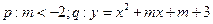 有两个不同的零点
有两个不同的零点 是偶函数
是偶函数

 个单位长度可以得到函数
个单位长度可以得到函数 的图像。
的图像。 是
是 的充分而不必要条件。
的充分而不必要条件。 , q:
, q: ,则p是q的
,则p是q的