题目内容
袋中有形状、质地都相同的黑球、白球和红球共10只,已知从袋中任意摸出一个球,得到黑球的概率为 ,从袋中任意摸出两个球,至少得到一个白球的概率为
,从袋中任意摸出两个球,至少得到一个白球的概率为 .
.
求(1)从袋中任意摸出两个球,至少得到一个黑球的概率;
(2)袋中白球的个数;
理(3)从袋中任意摸出三个球,记得到白球的个数为ξ,写出随机变量ξ的分布列,并求其数学期望Eξ
解:(1)由题意可得:袋中的黑球有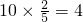 ,所以其他球有6个,所以从袋中任意摸出两个球,至少得到一个黑球的概率为
,所以其他球有6个,所以从袋中任意摸出两个球,至少得到一个黑球的概率为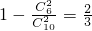 ;
;
(2)设袋中白球数为n.
设从中任摸2个球至少得到1个白球为事件A,任取两球无白球为事件 ,∴
,∴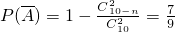 ,解得n=5,即袋中有5个白球;
,解得n=5,即袋中有5个白球;
(3)随机变量ξ的取值为0,1,2,3,分布列是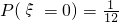 ,
,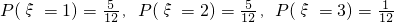
∴ξ的数学期望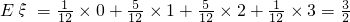 .
.
分析:(1)先求袋中的黑球的个数,从而得到其它求的个数,再利用对立事件求概率;
(2)根据从中任意摸出2个球,至少得到1个白球的概率是 ,写出从袋中任意摸出两个球,至少得到一个白球的对立事件的概率,列出关于白球个数的方程,解方程即可.
,写出从袋中任意摸出两个球,至少得到一个白球的对立事件的概率,列出关于白球个数的方程,解方程即可.
(3)从袋中任意摸出3个球,白球的个数为ξ,根据题意得到变量可能的取值,结合对应的事件,写出分布列和期望.
点评:本题的考点是离散型随机变量的期望与方差,主要考查排列组合、概率等基础知识,同时考查逻辑思维能力和数学应用能力,考查对立事件的概率,考查古典概型问题,是一个综合题.
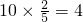 ,所以其他球有6个,所以从袋中任意摸出两个球,至少得到一个黑球的概率为
,所以其他球有6个,所以从袋中任意摸出两个球,至少得到一个黑球的概率为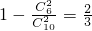 ;
;(2)设袋中白球数为n.
设从中任摸2个球至少得到1个白球为事件A,任取两球无白球为事件
 ,∴
,∴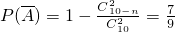 ,解得n=5,即袋中有5个白球;
,解得n=5,即袋中有5个白球;(3)随机变量ξ的取值为0,1,2,3,分布列是
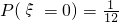 ,
,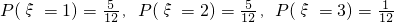
∴ξ的数学期望
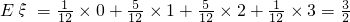 .
.分析:(1)先求袋中的黑球的个数,从而得到其它求的个数,再利用对立事件求概率;
(2)根据从中任意摸出2个球,至少得到1个白球的概率是
 ,写出从袋中任意摸出两个球,至少得到一个白球的对立事件的概率,列出关于白球个数的方程,解方程即可.
,写出从袋中任意摸出两个球,至少得到一个白球的对立事件的概率,列出关于白球个数的方程,解方程即可.(3)从袋中任意摸出3个球,白球的个数为ξ,根据题意得到变量可能的取值,结合对应的事件,写出分布列和期望.
点评:本题的考点是离散型随机变量的期望与方差,主要考查排列组合、概率等基础知识,同时考查逻辑思维能力和数学应用能力,考查对立事件的概率,考查古典概型问题,是一个综合题.

练习册系列答案
相关题目
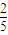 ,从袋中任意摸出两个球,至少得到一个白球的概率为
,从袋中任意摸出两个球,至少得到一个白球的概率为 .
.