题目内容
如果函数f(x)对于任意x∈R,存在M使不等式|f(x)|≤M|x|恒成立(其中M是与x无关的正常数),则称函数f(x)为有界泛函,给出下列函数:
①f1(x)=1;
②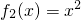 ;
;
③ ;
;
④f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f1(x)-f2(x)|≤2|x1-x2|,其中属于有界泛函的是________(填上正确序号).
③④
分析:根据有界泛函数的定义,逐个验证,对于①取x=0,即可说明①不是有界泛函数;对于②采取反证法,f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,得到矛盾,因此②不是有界泛函数;对于③求函数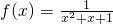 的最大值即可证明③是有界泛函数;对于④,通过取x2=0,如此可得到正确结论.从而得到答案.
的最大值即可证明③是有界泛函数;对于④,通过取x2=0,如此可得到正确结论.从而得到答案.
解答:函数f(x)对任意的实数x,存在常数M,使得不等式|f(x)|≤M|x|恒成立,那么就称函数f(x)为有界泛函数,
①取x=0,则|f(x)|=1,|x|=0,故不存在常数M,使得不等式|f(x)|≤M|x|成立,因此①不是有界泛函数;
②若f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,则有(M+1)2>M(M+1),故与假设矛盾,因此②不是有界泛函数;
③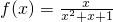 ≤
≤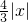 ,故④是有界泛函数;
,故④是有界泛函数;
④当x=0,因||f(x1)-f(x2)|≤2|x1-x2|得到|f(x)|≤2|x|成立,这样的M存在,故正确;
故答案为:③④.
点评:此题是个中档题.考查函数恒成立问题,以及三角函数的有界性和二次函数配方法求最值等基础知识,同时考查了学生的阅读能力,对题意的理解和转化能力,以及灵活应用知识分析解决问题的能力.
分析:根据有界泛函数的定义,逐个验证,对于①取x=0,即可说明①不是有界泛函数;对于②采取反证法,f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,得到矛盾,因此②不是有界泛函数;对于③求函数
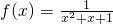 的最大值即可证明③是有界泛函数;对于④,通过取x2=0,如此可得到正确结论.从而得到答案.
的最大值即可证明③是有界泛函数;对于④,通过取x2=0,如此可得到正确结论.从而得到答案.解答:函数f(x)对任意的实数x,存在常数M,使得不等式|f(x)|≤M|x|恒成立,那么就称函数f(x)为有界泛函数,
①取x=0,则|f(x)|=1,|x|=0,故不存在常数M,使得不等式|f(x)|≤M|x|成立,因此①不是有界泛函数;
②若f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,则有(M+1)2>M(M+1),故与假设矛盾,因此②不是有界泛函数;
③
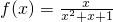 ≤
≤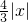 ,故④是有界泛函数;
,故④是有界泛函数;④当x=0,因||f(x1)-f(x2)|≤2|x1-x2|得到|f(x)|≤2|x|成立,这样的M存在,故正确;
故答案为:③④.
点评:此题是个中档题.考查函数恒成立问题,以及三角函数的有界性和二次函数配方法求最值等基础知识,同时考查了学生的阅读能力,对题意的理解和转化能力,以及灵活应用知识分析解决问题的能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ;
; ;
;