题目内容
已知条件p:“函数g(x)=logm(x-1)为减函数;条件q:关于x的二次方程
-2x+m=0有解,则p是q的( )
| x | 2 |
分析:由题意分别可得p:0<m<1,q:m≤1,由集合{m|0<m<1}和集合{m|m≤1}的包含关系可得答案.
解答:解:条件p“函数g(x)=logm(x-1)为减函数,则0<m<1;
条件q:关于x的二次方程
-2x+m=0有解,
则△=(-2)2-4m≥0,解得m≤1;
因为集合{m|0<m<1}是集合{m|m≤1}的真子集,
故p是q的充分不必要条件,
故选A
条件q:关于x的二次方程
| x | 2 |
则△=(-2)2-4m≥0,解得m≤1;
因为集合{m|0<m<1}是集合{m|m≤1}的真子集,
故p是q的充分不必要条件,
故选A
点评:本题考查充分必要条件的判断,从集合的包含关系入手是解决问题的关键,属基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
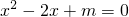 有解,则p是q的
有解,则p是q的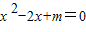 有解,则p是q的( )
有解,则p是q的( )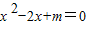 有解,则p是q的( )
有解,则p是q的( )