题目内容
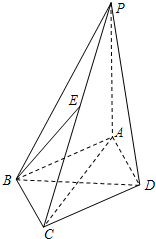 (2012•台州一模)如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=4
(2012•台州一模)如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=4| 3 |
(Ⅰ)当点E为线段PC的中点时,求证:BE⊥AC;
(Ⅱ)若二面角B-EA-D为直二面角,求直线BE与平面ABCD所成角的正切值.
分析:(Ⅰ)设AC与BD交于点O,当点E为线段PC的中点时,EO∥PA,从而可得EO⊥平面ABCD,进而有AC⊥EO,利用四边形ABCD是菱形,可得AC⊥BD,进而可得AC⊥平面BED,即可证明BE⊥AC;
(Ⅱ)解法1,向量法,利用二面角B-EA-D为直二面角,可得平面AED的一个法向量、平面ABE的一个法向量,数量积为0,进而利用向量的夹角公式,可求直线BE与平面ABCD所成角的正切值;
解法2:在三角形ABE中,作BF⊥EA,垂足为F,连接DF,OF,取线段CO的中点G,证明∠EBG就是直线BE与平面ABCD所成的角,即可求得结论.
(Ⅱ)解法1,向量法,利用二面角B-EA-D为直二面角,可得平面AED的一个法向量、平面ABE的一个法向量,数量积为0,进而利用向量的夹角公式,可求直线BE与平面ABCD所成角的正切值;
解法2:在三角形ABE中,作BF⊥EA,垂足为F,连接DF,OF,取线段CO的中点G,证明∠EBG就是直线BE与平面ABCD所成的角,即可求得结论.
解答:(Ⅰ)证明:设AC与BD交于点O,则O为AC,BD的中点,
因为点E为线段PC的中点,所以EO∥PA..…(1分)
又PA⊥平面ABCD,所以EO⊥平面ABCD,
所以AC⊥EO.…(3分)
因为四边形ABCD为菱形,所以AC⊥BD,BD∩EO=O,
所以AC⊥平面BED,…(5分)
因为BE⊆平面BED,所以BE⊥AC. …(6分)
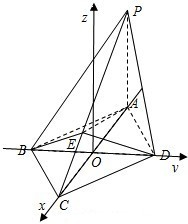
(Ⅱ)解法1:如图建立空间直角坐标系O-xyz,
则A(-2,0,0),B(0,-1,0),C(2,0,0),D(0,1,0),P(-2,0,4
),
所以
=(2,1,0),
=(2,-1,0).
设
=λ
(0≤λ≤1),
则
=
-
=(4λ,0,4
(1-λ)).
设平面AED的法向量
为(x,y,z),
则
取x=1得y=-2,
所以平面AED的一个法向量
为(1,-2,
); …(8分)
同理平面ABE的一个法向量
为(1,2,
); …(10分)
因为平面BEA⊥平面DEA,
所以
•
=-3+
=0,
得λ=
>1(舍去),λ=
∈(0,1),…(12分)
所以
=
+
=(1,1,
).
又因为平面ABCD的一个法向量
为(0,0,1),
所以cos<
,n3>=
,…(14分)
故直线BE与平面ABCD所成角的正切值为
.…(15分)
解法2:如图,在三角形ABE中,作BF⊥EA,垂足为F,连接DF,OF,
因为平面ABE⊥平面ADE,则BF⊥平面ADE,BF⊥FD.
因为OF=BO=DO=1,BD⊥AC,BD⊥PA,
所以BD⊥面PAC,面PAC⊥面ABC,BD⊥AE…(8分)
所以AE⊥平面BDF,所以OF⊥FA,
因为OA=2,所以∠FOA=60°,因为∠PCA=60°,
所以PC∥OF,CE⊥AE.…(10分)
所以CE=
AC=2,取线段CO的中点G,
则EG⊥AC,EG⊥面ABCD,
所以∠EBG就是直线BE与平面ABCD所成的角.…(12分)
因为CG=1,EG=
,BG=
,
所以tan∠EBG=
.
故直线BE与平面ABCD所成角的正切值为
.…(15分)
因为点E为线段PC的中点,所以EO∥PA..…(1分)
又PA⊥平面ABCD,所以EO⊥平面ABCD,
所以AC⊥EO.…(3分)
因为四边形ABCD为菱形,所以AC⊥BD,BD∩EO=O,
所以AC⊥平面BED,…(5分)
因为BE⊆平面BED,所以BE⊥AC. …(6分)
(Ⅱ)解法1:如图建立空间直角坐标系O-xyz,
则A(-2,0,0),B(0,-1,0),C(2,0,0),D(0,1,0),P(-2,0,4
| 3 |

所以
| AD |
| AB |
设
| PE |
| PC |
则
| AE |
| PE |
| PA |
| 3 |
设平面AED的法向量
| n1 |
则
|
取x=1得y=-2,
所以平面AED的一个法向量
| n1 |
| λ | ||
(λ-1)
|
同理平面ABE的一个法向量
| n2 |
| λ | ||
(λ-1)
|
因为平面BEA⊥平面DEA,
所以
| n1 |
| n2 |
| λ2 |
| 3(λ-1)2 |
得λ=
| 3 |
| 2 |
| 3 |
| 4 |
所以
| BE |
| BP |
| PE |
| 3 |
又因为平面ABCD的一个法向量
| n3 |
所以cos<
| BE |
| ||
|
故直线BE与平面ABCD所成角的正切值为
| ||
| 2 |
解法2:如图,在三角形ABE中,作BF⊥EA,垂足为F,连接DF,OF,
因为平面ABE⊥平面ADE,则BF⊥平面ADE,BF⊥FD.

因为OF=BO=DO=1,BD⊥AC,BD⊥PA,
所以BD⊥面PAC,面PAC⊥面ABC,BD⊥AE…(8分)
所以AE⊥平面BDF,所以OF⊥FA,
因为OA=2,所以∠FOA=60°,因为∠PCA=60°,
所以PC∥OF,CE⊥AE.…(10分)
所以CE=
| 1 |
| 2 |
则EG⊥AC,EG⊥面ABCD,
所以∠EBG就是直线BE与平面ABCD所成的角.…(12分)
因为CG=1,EG=
| 3 |
| 2 |
所以tan∠EBG=
| ||
| 2 |
故直线BE与平面ABCD所成角的正切值为
| ||
| 2 |
点评:本题考查线面垂直,考查线线垂直,考查线面角,考查向量法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目