题目内容
空间有五个点,其中三个点在同一直线上,其他任何三点不在同一直线上,则可以确定
5
5
个平面.分析:设共线的三点为A,B,C,另外不共线的两点为D,E,通过讨论确定平面的个数即可.
解答:解:因为空间有五个点,其中三个点在同一直线上,其他任何三点不在同一直线上,则设共线的三点为A,B,C,另外不共线的两点为D,E.
若共线的三点中,只选1个点,则DAB,DBE,DCE,各确定一个平面.
若共线的三点中,选取2点共面,则DABC,和EABC,各确定一个平面,所以共有5个平面.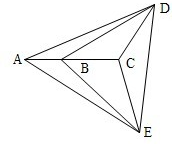
故答案为:5.
若共线的三点中,只选1个点,则DAB,DBE,DCE,各确定一个平面.
若共线的三点中,选取2点共面,则DABC,和EABC,各确定一个平面,所以共有5个平面.

故答案为:5.
点评:本题考查平面的基本性质及其推论,是基础题.要注意分类讨论.

练习册系列答案
相关题目
空间有五个点,其中有四个点在同一平面内,但没有任何三点共线,这样五个点,最多可以确定的平面个数是
[
]|
A .4个 |
B .5个 |
C .6个 |
D .7个 |