题目内容
求圆心在直线3x+y-5=0上,并且经过原点和点(4,0)的圆的方程.
【答案】分析:由直线和圆相交的性质可得,圆心在点O(0,0)和点A(4,0)的中垂线x=2上,再根据圆心在直线3x+y-5=0上,可得圆心C的坐标和半径r=|OC|的值,从而得到所求的圆的方程.
解答:解:由直线和圆相交的性质可得,圆心在点O(0,0)和点A(4,0)的中垂线x=2上,
再根据圆心在直线3x+y-5=0上,可得圆心C的坐标为(2,-1),故半径r=|OC|=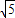 ,
,
故所求的圆的方程为 (x-2)2+(y+1)2=5.
点评:本题主要考查直线和圆相交的性质,求圆的标准方程,求出圆心坐标,是解题的关键,属于中档题.
解答:解:由直线和圆相交的性质可得,圆心在点O(0,0)和点A(4,0)的中垂线x=2上,
再根据圆心在直线3x+y-5=0上,可得圆心C的坐标为(2,-1),故半径r=|OC|=
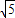 ,
,故所求的圆的方程为 (x-2)2+(y+1)2=5.
点评:本题主要考查直线和圆相交的性质,求圆的标准方程,求出圆心坐标,是解题的关键,属于中档题.

练习册系列答案
相关题目