Question

已知曲线

（1）求证：不论取何实数，曲线恒过一定点；

（2）证明：当时，曲线是一个圆，且圆心在一条定直线上；

（3）若曲线与轴相切，求的值．

Answer 1

（１）曲线恒过定点．（２）圆心在直线上．（3）．

解析:

（１）证明：曲线的方程可化为：

由，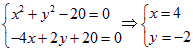

不论取何值时，，总适合曲线的方程，即曲线恒过定点．

（２）证明：，，，

．

，，，

曲线是一个圆，设圆心坐标为．

则由消去得，即圆心在直线上．

（3）若曲线与轴相切，则，曲线为圆，其半径，又圆心为，则，．