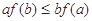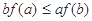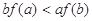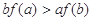题目内容
已知函数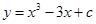 的图像与
的图像与 轴恰有两个公共点,则
轴恰有两个公共点,则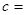 ( )
( )
| A.-2或2 | B.-9或3 | C.-1或1 | D.-3或1 |
A.
解析试题分析:对函数进行求导即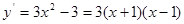 ,确定函数的单调性并判断函数的极值点,即令
,确定函数的单调性并判断函数的极值点,即令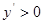 ,可得
,可得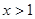 或
或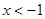 ;令
;令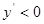 ,可得
,可得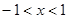 ;于是知函数在
;于是知函数在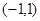 上单调递减,在
上单调递减,在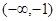 ,
,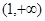 上单调递增,所以函数在
上单调递增,所以函数在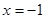 处取得极大值,在
处取得极大值,在 处取得极小值.利用函数
处取得极小值.利用函数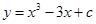 的图像与
的图像与 轴恰有两个公共点知,极大值等于0或极小值等于0,由此可解出
轴恰有两个公共点知,极大值等于0或极小值等于0,由此可解出 的值.
的值.
考点:利用导数研究函数的极值;函数的零点与方程根的关系.

练习册系列答案
相关题目
若函数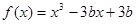 在(0,1)内有极小值,则 ( )
在(0,1)内有极小值,则 ( )
A.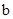 <1 <1 | B.0< <1 <1 | C.b>0 | D.b< |
函数f(x)=ax3-x在R上为减函数,则( )
| A.a≤0 | B.a<1 | C.a<0 | D.a≤1 |
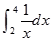 等于( )
等于( )
A. | B.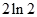 | C.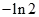 | D. |
设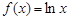 ,若
,若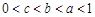 ,则
,则 ,
, ,
,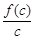 的大小关系为( )
的大小关系为( )
A. |
B.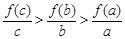 |
C.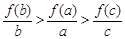 |
D.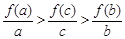 |
函数 的部分图像如图所示,则
的部分图像如图所示,则 的解析式可以是( )
的解析式可以是( )
A.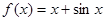 |
B. |
C.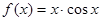 |
D. |
一物体的运动方程为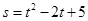 ,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
| A.8米/秒 | B.7米/秒 | C.6米/秒 | D.5米/秒 |
一物体在力 (单位:N)的作用下沿与力
(单位:N)的作用下沿与力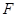 相同的方向,从x=0处运动到
相同的方向,从x=0处运动到 (单位:
(单位:  )处,则力
)处,则力 做的功为( )
做的功为( )
| A.44 | B.46 | C.48 | D.50 |
 定义在
定义在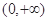 上的非负可导函数,且满足
上的非负可导函数,且满足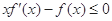 ,对任意正数
,对任意正数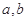 , 若
, 若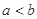 ,则必有( ).
,则必有( ).