题目内容
（本小题12分）某电视节目《幸运猜猜猜》有这样一个竞猜环节，一件价格为9816元的商品，选手只知道1,6,8,9四个数，却不知其顺序，若在竞猜中猜出正确价格中的两个或以上（但不含全对）正确位置，则正确位置会点亮红灯作为提示；若全对，则所有位置全亮白灯并选手赢得该商品，
（Ⅰ）求某选手在第一次竞猜时，亮红灯的概率；
（Ⅱ）若该选手只有二次机会，则他赢得这件商品的概率为多少？
【答案】
（Ⅰ）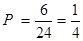
；（Ⅱ）
。
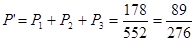【解析】本试题主要是考查了古典概型概率的求解，以及互斥事件概率的加法公式的综合运用。
（1）由于1，6，8，9能排列出24种情况，其中2个位置正确的有6种，而却没有3个位置全部正确，故可得。
（2）因为赢得商品分三类，①第一次猜对，概率为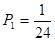
,②第一次亮红灯，则可分析的剩下的2个位置必定是填反了数字，所以在第一次亮红灯的情况下，第二次必定正确，则
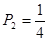，③第一次没有亮红灯，而第二次全部猜中，
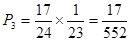，利用互斥事件概率加法公式得到。，
解：（Ⅰ）1，6，8，9能排列出24种情况，其中2个位置正确的有6种，而却没有3个位置全部正确，所以第一次竞猜时亮红灯的概率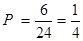……………….6分
（Ⅱ）赢得商品分三类，①第一次猜对，概率为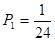,②第一次亮红灯，则可分析的剩下的2个位置必定是填反了数字，所以在第一次亮红灯的情况下，第二次必定正确，则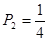，③第一次没有亮红灯，而第二次全部猜中，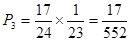
所以，二次能赢得商品的的概率为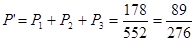……………….12分
练习册系列答案
相关题目
个月的旅游人数的和
（单位：万人）与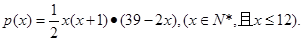
已知第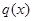
（单位：元）与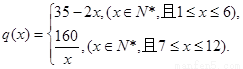
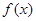（单位：万人）与x的函数关系式；
万元，每生产
（
）千件，需另投入成本为
，当年产量不足
千件时，
（万元）；当年产量不小于
（万元）.通过市场分析，若每件售价为
元时，该厂年内生产该商品能全部销售完. 
（万元）关于年产量