题目内容
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB. (Ⅰ)求证:平面PAB⊥平面PCB;
(Ⅱ)求证:PD∥平面EAC;
(Ⅲ)求平面AEC和平面PBC所成锐二面角的余弦值.
【答案】(Ⅰ)证明:∵PA⊥底面ABCD,BC底面ABCD, ∴PA⊥BC.
又AB⊥BC,PA∩AB=A,
∴BC⊥平面PAB.
又BC平面PCB,∴平面PAB⊥平面PCB.
(Ⅱ)证明:∵PC⊥AD,
∴在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC= ![]() ,
,
∴∠DCA=∠BAC= ![]() ,
,
又AC⊥AD,
故△DAC为等腰直角三角形,
∴DC= ![]() AC=
AC= ![]() (
( ![]() AB)=2AB.
AB)=2AB.
连接BD,交AC于点M,则 ![]() =
= ![]() =2.
=2.
连接EM,在△BPD中, ![]() =
= ![]() =2,∴PD∥EM,
=2,∴PD∥EM,
又PD/平面EAC,EM平面EAC,
∴PD∥平面EAC.
(Ⅲ)解:以A为坐标原点,AB,AP所在直线分别为y轴,z轴,建立如图所示的空间直角坐标系.则A(0,0,0),B(0,3,0),C(3,3,0),P(0,0,3),E(0,2,1)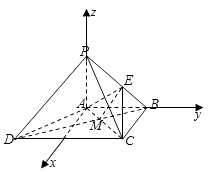
设 ![]() =(x,y,1)为平面AEC的一个法向量,则
=(x,y,1)为平面AEC的一个法向量,则 ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
,
∵ ![]() =(3,3,0),
=(3,3,0), ![]() =(0,2,1),
=(0,2,1),
∴ ![]() 解得x=
解得x= ![]() ,y=﹣
,y=﹣ ![]() ,
,
∴ ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,1).
,1).
设 ![]() =(x′,y′,1)为平面PBC的一个法向量,则
=(x′,y′,1)为平面PBC的一个法向量,则 ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
,
又 ![]() =(3,0,0),
=(3,0,0), ![]() =(0,﹣3,3),
=(0,﹣3,3),
∴ ![]() ,
,
解得x′=0,y′=1,
∴ ![]() =(0,1,1).
=(0,1,1).
(取PB中点为F,连接AF可证 ![]() 为平面PBC的一个法向量.)
为平面PBC的一个法向量.)
∵cos< ![]() ,
, ![]() >=
>=  =
= ![]() ,
,
∴平面AEC和平面PBC所成锐二面角的余弦值为 ![]()
注:以其他方式建系的参照给分.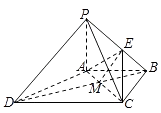
【解析】(Ⅰ)根据PA⊥底面ABCD,得到PA⊥BC,结合AB⊥BC,可得BC⊥平面PAB.最后根据面面垂直的判定定理,可证出平面PAB⊥平面PCB.(Ⅱ)利用线面垂直的性质,可得在直角梯形ABCD中AC⊥AD,根据题中数据结合平行线分线段成比例,算出DC=2AB,从而得到△BPD中,PE:EB=DM:MB=2,所以PD∥EM,由线面平行的判定定理可得PD∥平面EAC.(Ⅲ)建立空间直角坐标系,求出平面AEC、平面PBC的一个法向量,利用向量的夹角公式,即可求平面AEC和平面PBC所成锐二面角的余弦值.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直)的相关知识才是答题的关键.

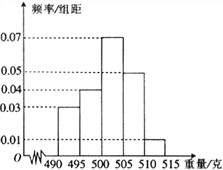
【题目】国际奥委会于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | _______ | _______ | 80 |
年龄大于50岁 | 10 | _______ | _______ |
合计 | _______ | 70 | 100 |
(1)根据已知数据,把表格填写完整;
(2)是否有95%的把握认为年龄与支持申办奥运有关?
附表:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.814 | 5.024 | 6.635 |