题目内容
求经过点(-3,4),并且在两坐标轴上截距之和为12的直线的一般式方程.
分析:设出直线的截距式方程,根据题意建立直线在两轴上的截距a、b的方程组,解之即可得到所求直线的方程.
解答:解:设直线的方程为
+
=1(ab≠0)
根据题意,得
解之此方程组,得a=9、b=3或a=-4、b=16
∴直线的方程为
+
=1或
+
=1,
化简得x+3y-9=0或4x-y+16=0.
| x |
| a |
| y |
| b |
根据题意,得
|
解之此方程组,得a=9、b=3或a=-4、b=16
∴直线的方程为
| x |
| 9 |
| y |
| 3 |
| x |
| -4 |
| y |
| 16 |
化简得x+3y-9=0或4x-y+16=0.
点评:本题给出直线经过定点,在满足截距之和等于12的情况下求直线的方程.着重考查了直线的方程和直线的截距等知识,属于基础题.

练习册系列答案
相关题目
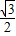 ,两个焦点分别为F1和F2,椭圆G上一点到F1和F2的距离之和为12.圆C:x2+y2+2x-4y-20=0的圆心为点A.
,两个焦点分别为F1和F2,椭圆G上一点到F1和F2的距离之和为12.圆C:x2+y2+2x-4y-20=0的圆心为点A.