题目内容
设y=f(x)是R上的奇函数.
f(x+2)=-f(x).当-1≤x≤1时,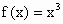 .
.
(1)试证:直线x=1是函数y=f(x)图象的对称轴;
(2)试求xÎ [1,5)时,f(x)解析式;
(3)若A={x||f(x)|>a,xÎ
R,且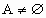 ,求实数a的取值范围.
,求实数a的取值范围.
答案:略
解析:
解析:
|
(1) ∵f(1+x)=f[2+(x-1)]=-f(x-1)=f(1-x),∴ y=f(x)的图象关于直线x=1对称.(2) 当xÎ [1,3]时,2-xÎ [-1,1],则 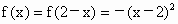 , ,
当 xÎ [3,5]时,x-2Î [1,3],则 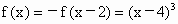 . .
∴ 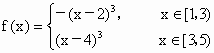
(3)f(x +4)=-f(x+2)=f(x),∴ f(x)是以4为周期的函数.∴ {y|y=f(x),xÎ R}={y|y=f(x),1≤x≤5},∵ f(x)在[1,3]上是减函数,∴-1≤f(x)≤1;又 f(x)在[3,5]上是增函数,∴- 1≤f(x)≤1,∴f(x)的值域为[-1,1],即 |f(x)|≤1,故a<1. |

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
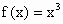 .
.
 ,求实数a的取值范围.
,求实数a的取值范围.
 B.0 C.
B.0 C. B.0 C.
B.0 C.