题目内容
设
为抛物线
上任一点，
为焦点，则以
为直径的圆与
轴的位置关系是 。
以
为直径的圆与
轴的位置关系是相切。
解析:
设
，∵
，∴以
为直径的圆的圆心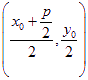为
，半径为
，∵
点在抛物线上，∴
，∴
=
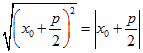，恰好等于圆心到轴的距离，∴以为直径的圆与轴的位置关系是相切。
练习册系列答案
相关题目
解析:
题目内容
设为抛物线上任一点，为焦点，则以为直径的圆与轴的位置关系是 。
以为直径的圆与轴的位置关系是相切。
设，∵，∴以为直径的圆的圆心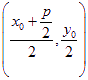为，半径为，∵点在抛物线上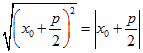，∴，∴=，恰好等于圆心到轴的距离，∴以为直径的圆与轴的位置关系是相切。