题目内容
无论m取任何实数值,方程|x2-3x+2|=m(x-
)的实根个数是( )
| 3 |
| 2 |
分析:要求方程|x2-3x+2|=m(x-
)的实根个数,就是函数y=|x2-3x+2|、与直线y=m(x-
)交点的个数,画出函数y=|x2-3x+2|的图象,根据直线y=m(x-
)过定点(
,0),即可求得结果.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:方程|x2-3x+2|=m(x-
)的实根个数,就是函数y=|x2-3x+2|与直线y=m(x-
)交点的个数,
画出函数y=|x2-3x+2|的图象如图所示,
而直线y=m(x-
)过定点(
,0),
因此m不论取任何实数值,函数y=|x2-3x+2|与直线y=m(x-
)总是有两个交点,
即方程|x2-3x+2|=m(x-
)的实根个数是2.
故选B.
| 3 |
| 2 |
| 3 |
| 2 |
画出函数y=|x2-3x+2|的图象如图所示,

而直线y=m(x-
| 3 |
| 2 |
| 3 |
| 2 |
因此m不论取任何实数值,函数y=|x2-3x+2|与直线y=m(x-
| 3 |
| 2 |
即方程|x2-3x+2|=m(x-
| 3 |
| 2 |
故选B.
点评:本题重点考查根的存在性和根的个数的判定,考查方程的根与函数图象交点之间的关系,体现了转化的思想和数形结合的思想,正确转化,利用函数的图象是关键

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 的实根个数是( )
的实根个数是( )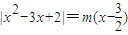 的实根个数是( )
的实根个数是( )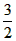 )的实数根的个数都是
)的实数根的个数都是