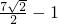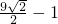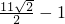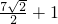Question

若曲线y=2x-x³在横坐标为-1的点处的切线为l，则圆（x-3）²+（y-2）²=1上任意一点到直线l的距离的最小值为（　　）

• A．

  7 2

  2

  -1
• B．

  9 2

  2

  -1
• C．

  11 2

  2

  -1
• D．

  7 2

  2

  +1

Answer 1

分析：将-1代解析式求得切点的坐标，再求出y=2x-x³的导数，将-1代入求出切线的斜率，由点斜式求出切线的方程，整理成一般式，点到直线的距离公式求出距离，最后减去半径即可求出所求．

解答：解：∵y=2x-x³
∴y'=2-3x²
又切点的横坐标为-1，故切点的纵坐标是-1，y'=-1
故切线的方程是y+1=-（x+1），即切线的方程是x+y+2=0
所以圆心（3，2）到直线l的距离d=

7

2

=

7 2

2

∴圆（x-3）²+（y-2）²=1上任意一点到直线l的距离的最小值为

7 2

2

-1
故选A．

点评：本题考查利用导数研究曲线上某点切线方程，点到直线的距离公式，同时考查了运算求解的能力，属于中档题．