题目内容
已知射线OP分别与OA、OB都成
的角,∠A0B=
,则OP与平面AOB所成的角等于( )
| π |
| 4 |
| π |
| 3 |
分析:设点P在平面AOB中的射影为D,由射线OP分别与OA、OB都成
的角,∠A0B=
,知OD是∠AOB的平分线,∠POD是OP与平面AOB所成的角,故∠AOD=
,由三余弦定理cos∠POB=cos∠POD•cos∠AOD,能求出OP与平面AOB所成的角.
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
解答:解:设点P在平面AOB中的射影为D,
∵射线OP分别与OA、OB都成
的角,∠A0B=
,
∴OD是∠AOB的平分线,∠POD是OP与平面AOB所成的角,
∴∠AOD=
,
由三余弦定理知cos∠POB=cos∠POD•cos∠AOD,
∴cos∠POD=
=
=
=
,
∴∠POD=arccos
.
故选D.
∵射线OP分别与OA、OB都成
| π |
| 4 |
| π |
| 3 |
∴OD是∠AOB的平分线,∠POD是OP与平面AOB所成的角,
∴∠AOD=
| π |
| 6 |
由三余弦定理知cos∠POB=cos∠POD•cos∠AOD,
∴cos∠POD=
| cos∠POB |
| cos∠AOD |
cos
| ||
cos
|
| ||||
|
| ||
| 3 |
∴∠POD=arccos
| ||
| 3 |
故选D.
点评:本题考查直线与平面所成的角的大小的求法,解题时要认真审题,仔细解答,注意三余弦定理的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
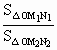 =
=