题目内容
设Sn是等差数列的{an}前n项和,且S9=18,Sn=240,若an-4=30(n>9),则n的值为
- A.13
- B.14
- C.15
- D.16
C
分析:由等差数列前n项和公式,等差数列的性质,得出a 5=2,a 5+an-4=a1+an=32,代入前n项和公式求出n即可.
解答:根据等差数列前n项和公式,S9=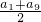 ×9=18,
×9=18,
又根据等差数列的性质,a1+a9=2a5,
∴S9=9a5,
∴a 5=2,
∴a 5+an-4=32.
∴a1+an=32
∴Sn=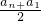 ×n=240,
×n=240,
解得n=15.
故选C
点评:本题考查差数列前n项和公式的灵活应用,等差数列的性质.利用等差数列的性质,进行整体代换,使问题巧妙获解.
分析:由等差数列前n项和公式,等差数列的性质,得出a 5=2,a 5+an-4=a1+an=32,代入前n项和公式求出n即可.
解答:根据等差数列前n项和公式,S9=
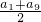 ×9=18,
×9=18,又根据等差数列的性质,a1+a9=2a5,
∴S9=9a5,
∴a 5=2,
∴a 5+an-4=32.
∴a1+an=32
∴Sn=
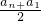 ×n=240,
×n=240,解得n=15.
故选C
点评:本题考查差数列前n项和公式的灵活应用,等差数列的性质.利用等差数列的性质,进行整体代换,使问题巧妙获解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 的前n项和,若
的前n项和,若 ( )
( )
 的前n项和,已知
的前n项和,已知 ,
, ,则
,则 等于( )
等于( ) 的前n项和,若S7 = 35,则a4 的值为( )
的前n项和,若S7 = 35,则a4 的值为( )