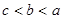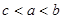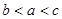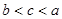题目内容
已知x满足a2x+a6≤ax+2+ax+4(0<a<1),函数y=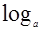 (
(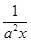 )·
)·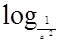 (ax)的值域为
(ax)的值域为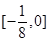 ,求a的值.
,求a的值.
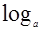 (
(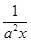 )·
)·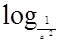 (ax)的值域为
(ax)的值域为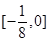 ,求a的值.
,求a的值. 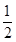
本试题主要是考查了函数的单调性质和指数函数与对数函数的化简运算的综合运用。
由a2x+a6≤ax+2+ax+4(0<a<1)
由y=loga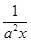 ·log
·log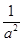 (ax)整理得
(ax)整理得
y=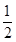
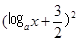 -
- .
.
∵y∈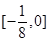 ,即
,即
- ≤
≤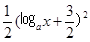 2-
2- ≤0,
≤0,
∴-2≤logax≤-1.
∵2≤x≤4,0<a<1,logax为单调减函数,
∴loga2≤-1且loga4≥-2⇒a=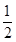 .
.
由a2x+a6≤ax+2+ax+4(0<a<1)
由y=loga
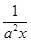 ·log
·log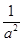 (ax)整理得
(ax)整理得y=
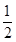
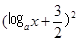 -
- .
.∵y∈
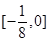 ,即
,即-
 ≤
≤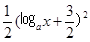 2-
2- ≤0,
≤0,∴-2≤logax≤-1.
∵2≤x≤4,0<a<1,logax为单调减函数,
∴loga2≤-1且loga4≥-2⇒a=
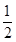 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
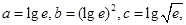 则
则 
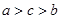
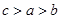
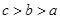
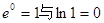
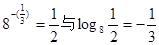
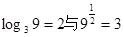
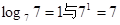
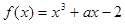 在区间
在区间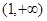 内是增函数,则实数
内是增函数,则实数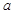 的取值范围
的取值范围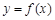 是函数
是函数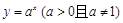 的反函数,其图象经过点
的反函数,其图象经过点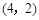 ,则
,则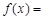 ______________.
______________.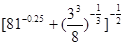
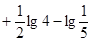 ;
;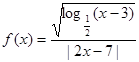 的定义域;
的定义域;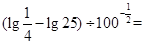
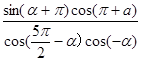 (2)求值
(2)求值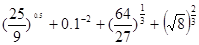
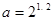 ,
,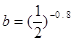 ,
,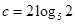 ,则
,则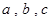 的大小关系为( )
的大小关系为( )