题目内容
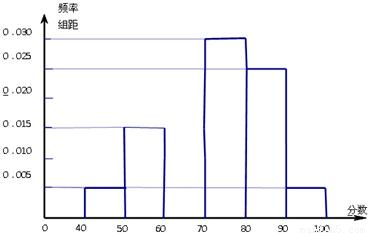
从高一年级中抽出50名学生参加数学竞赛,由成绩得到如下的频率分布直方图.
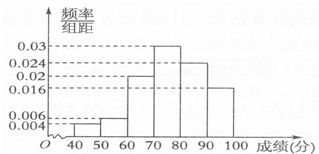
利用频率分布直方图估计:
(1)这50名学生的众数P与中位数M(精确到0.1);
(2)若在第3、5组的学生中,用分层抽样抽取11名学生参加心理测试,请问:在第3、5组各应抽取多少名学生参加测试;
(3)为了进一步获得研究资料,学校决定再从第1组和第2组的学生中,随机抽取3名学生进行心理测试,列出所有基本事件,并求
㈠第1组中的甲同学和第2组中的A同学都没有被抽到的概率;
㈡第1组中至多有一个同学入选的概率.

利用频率分布直方图估计:
(1)这50名学生的众数P与中位数M(精确到0.1);
(2)若在第3、5组的学生中,用分层抽样抽取11名学生参加心理测试,请问:在第3、5组各应抽取多少名学生参加测试;
(3)为了进一步获得研究资料,学校决定再从第1组和第2组的学生中,随机抽取3名学生进行心理测试,列出所有基本事件,并求
㈠第1组中的甲同学和第2组中的A同学都没有被抽到的概率;
㈡第1组中至多有一个同学入选的概率.
分析:(1)由频率分布直方图与众数、中位数的定义求出P=75,M=70;
(2)根据第三与第五组的频率,求出第三与第五组的人数,按比例计算可得;
(3)先求出第一、第二组的人数,再写出从中抽取3人的所有基本事件,分别找出符合(一),(二)的基本事件,利用古典概型求概率.
(2)根据第三与第五组的频率,求出第三与第五组的人数,按比例计算可得;
(3)先求出第一、第二组的人数,再写出从中抽取3人的所有基本事件,分别找出符合(一),(二)的基本事件,利用古典概型求概率.
解答:解:(1)由频率分布直方图知:众数P=75;中位数M=70,
(2)第3组共有学生50×0.02×10=10(人);第5组共有学生50×0.024×10=12(人)
抽取比例为
=
,∴第3组抽5人;第5组抽6人.
(3)第1组共50×0.004×10=2人,用甲、乙表示;
第2组共50×0.006×10=3人用A、B、C表示,则从这5名学生中随机抽取3名的所有可能为:(甲,乙,A)(甲,乙,B)(甲,乙,C)(甲,A,B)
(甲,A,C)(甲,B,C)(乙,A,B)(乙,A,C)(乙,B,C)(A、B、C)
共10个.
(一)事件S={第1组中的甲同学和第2组中的A同学都没有被抽到}其有(乙,B,C)共1个,所以P(S)=
.
(二)事件T={第1组中至多有一个同学入选}其有(甲,A,B)(甲,A,C)(甲,B,C)(乙,A,B)(乙,A,C)(乙,B,C)(A、B、C)共有7个,
所以P(T)=
.
(2)第3组共有学生50×0.02×10=10(人);第5组共有学生50×0.024×10=12(人)
抽取比例为
| 11 |
| 22 |
| 1 |
| 2 |
(3)第1组共50×0.004×10=2人,用甲、乙表示;
第2组共50×0.006×10=3人用A、B、C表示,则从这5名学生中随机抽取3名的所有可能为:(甲,乙,A)(甲,乙,B)(甲,乙,C)(甲,A,B)
(甲,A,C)(甲,B,C)(乙,A,B)(乙,A,C)(乙,B,C)(A、B、C)
共10个.
(一)事件S={第1组中的甲同学和第2组中的A同学都没有被抽到}其有(乙,B,C)共1个,所以P(S)=
| 1 |
| 10 |
(二)事件T={第1组中至多有一个同学入选}其有(甲,A,B)(甲,A,C)(甲,B,C)(乙,A,B)(乙,A,C)(乙,B,C)(A、B、C)共有7个,
所以P(T)=
| 7 |
| 10 |
点评:本题考查了利用频率分布直方图求众数、中位数;考查了分层抽样方法;考查了古典概型的概率计算,综合性较强.

练习册系列答案
相关题目
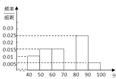 ,50),[50,60),…[90,100]后画出如图所示的部分频率分布直方图.观察图形的信息,回答下列问题:
,50),[50,60),…[90,100]后画出如图所示的部分频率分布直方图.观察图形的信息,回答下列问题: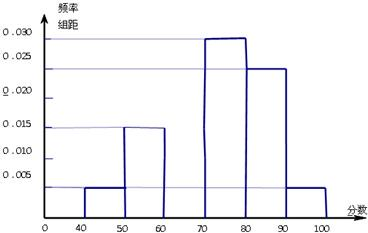
 (2010•马鞍山模拟)某校从高一年级期末考试学生中抽出60名学生的数学成绩,将其(均为整数)分成六组[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]画出部分频率分布直方图,由此估计期末考似高一年级数学的平均分为
(2010•马鞍山模拟)某校从高一年级期末考试学生中抽出60名学生的数学成绩,将其(均为整数)分成六组[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]画出部分频率分布直方图,由此估计期末考似高一年级数学的平均分为