题目内容
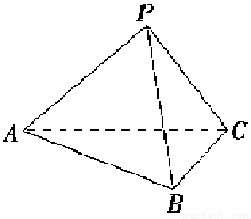
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为 .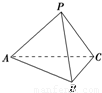
【答案】分析:取BC中点O,连接PO,AO,先证明BC⊥面APO,由此能求出异面直线PA与BC所成的角的大小.
解答: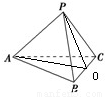 解:取BC中点O,连接PO,AO,
解:取BC中点O,连接PO,AO,
∵PA=PB=PC,且AB=AC,∠BAC=90°,
∴PO⊥BC,AO⊥BC,
∴BC⊥面APO,
∵AP?面APO,
∴AP⊥BC,
∴异面直线PA与BC所成的角为90°.
故答案为:90°.
点评:本题考查空间中异面直线所成角的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.
解答:
 解:取BC中点O,连接PO,AO,
解:取BC中点O,连接PO,AO,∵PA=PB=PC,且AB=AC,∠BAC=90°,
∴PO⊥BC,AO⊥BC,
∴BC⊥面APO,
∵AP?面APO,
∴AP⊥BC,
∴异面直线PA与BC所成的角为90°.
故答案为:90°.
点评:本题考查空间中异面直线所成角的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为