题目内容
抛物线![]() 的准线与坐标轴交于A点,过A作直线与抛物线交于M、N两点,点B在抛物线的对称轴上,且
的准线与坐标轴交于A点,过A作直线与抛物线交于M、N两点,点B在抛物线的对称轴上,且![]() 。
。
(Ⅰ)求![]() 的范围;
的范围;
(Ⅱ)是否存在这样的点B,使得△BMN为等腰直角三角形,且∠B=90º。若存在,求出点B;若不存在,说明理由。
解:(Ⅰ)抛物线为![]() ,准线为
,准线为![]() ,
,
∴A(0,-2)
设MN的中点为P,∵![]() ,
,
∴PB垂直平分线段MN
设MN为:![]() ,与
,与![]() 联立,得
联立,得
![]() (*)
(*)
由![]() ,
,
又点P坐标为:![]() ,
,
∴直线PB方程为:![]()
令![]() ,得
,得![]() ,
,
∴![]() 的取值范围是(6,+∞)
的取值范围是(6,+∞)
(Ⅱ)由![]() ,
,
解得,![]() ,
,
∴点B(0,10)为所求。

练习册系列答案
相关题目
 )•
)• =0.
=0.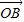 |的取值范围;
|的取值范围;