Question

如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆．在扇形OAB内随机取一点，则此点取自阴影部分的概率是

1-

2

π

．

Answer 1

分析：以面积为测度，计算出阴影的面积，扇形的面积，可求概率．

解答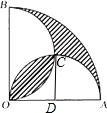：解：如图，设两个半圆的交点为C，且以AO为直径的半圆以D为圆心，连结OC、CD
设OA=OB=2，则弓形OMC的面积为
S_弓形OMC=S_扇形OCD-S_Rt△DCO=

1

4

•π•1²-

1

2

×1×1=

π

4

-

1

2

所以空白部分面积为S_空白=2（S_半圆AO-2S_弓形OMC）=2[

1

2

•π•1²-（

π

2

-1）]=2
因此，两块阴影部分面积之和为S_阴影=S_扇形OAB-S_空白=

1

4

π•2²-2=π-2
可得在扇形OAB内随机取一点，此点取自阴影部分的概率为P=

S阴影

S扇形OAB

=

π-2

π

=1-

2

π

．
故答案为：1-

2

π

．

点评：本题考查了扇形面积公式、组合图形的面积计算和几何概型计算公式等知识，属于中档题．