题目内容
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥平面ABCD,E在棱PB上.
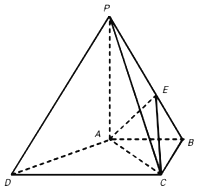
(Ⅰ)求证:AC⊥PD;
(Ⅱ)若VP﹣ACE![]() ,求证:PD∥平面AEC.
,求证:PD∥平面AEC.
【答案】(Ⅰ)见解析;(Ⅱ)见解析
【解析】
(I)过![]() 作
作![]() ,判断出四边形
,判断出四边形![]() 为则方程,由此证得
为则方程,由此证得![]() ,结合
,结合![]() 证得
证得![]() 平面
平面![]() ,从而证得
,从而证得![]() .
.
(II)利用题目所给体积求得![]() 到平面
到平面![]() 的距离,连接
的距离,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,通过证明
,通过证明![]() ,证得
,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(Ⅰ)过A作AF⊥DC于F,∵AB∥CD,AB⊥BC,AB=BC=1,∴四边形ABCF为正方形,则CF=DF=AF=1,
∴∠DAC=90°,得AC⊥DA,又PA⊥底面ABCD,AC平面ABCD,∴AC⊥PA,
又PA,AD平面PAD,PA∩AD=A,∴AC⊥平面PAD,又PD平面PAD,∴AC⊥PD;
(Ⅱ)设E到平面ABCD的距离为h,则VP﹣ACE![]() ,得h
,得h![]() .
.
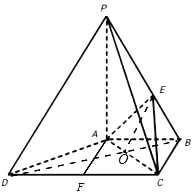
又PA=2,则PB:EB=PA:h=3:1.∵BC=1,CD=2,∴DB![]() ,连接DB交AC于O,连接OE,
,连接DB交AC于O,连接OE,
∵△AOB∽△COD,∴DO:OB=2:1,得DB:OB=3:1,
∴PB:EB=DB:OB,则PD∥OE.又OE平面AEC,PD平面AEC,∴PD∥平面AEC.

【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
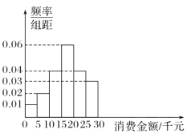
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |