Question

函数y=sinx的定义域是[a，b]，值域是[-1，-

1

2

]，则b-a的最大值与最小值之和是

π

．

Answer 1

分析：作出y=sinx，值域是[-1，-

1

2

]的图象，可知b-a的最大值与最小值，从而可得结论．

解答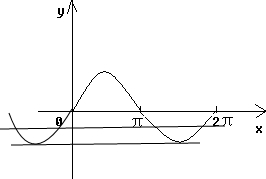：解：作出y=sinx，值域是[-1，-

1

2

]的图象：
可知b-a的最大值为

11π

6

-

7π

6

=

2π

3

，
b-a的最小值为

3π

2

-

7π

6

=

π

3

∴b-a的最大值与最小值之和是

2π

3

+

π

3

=π
故答案为：π

点评：本题考查了正弦函数的定义域和值域的关系，考查学生分析解决问题的能力，属于基础题．