题目内容
已知点O(0,0),A(1,2),B(4,5)及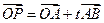 ,
,
求(1)t为何值时,P在x轴上?P在y轴上?P在第二象限。
(2)四边形OABP能否构成为平行四边形?若能,求出相应的t值;若不能,请说明理由。
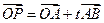 ,
,求(1)t为何值时,P在x轴上?P在y轴上?P在第二象限。
(2)四边形OABP能否构成为平行四边形?若能,求出相应的t值;若不能,请说明理由。
略
(1) 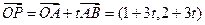 ,若P在x轴上,只需
,若P在x轴上,只需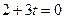 ,∴
,∴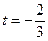 ;
;
若P 在y轴上,只需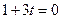 ,∴
,∴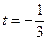 ;
;
若P在第二象限,只需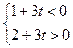 ∴
∴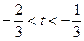
(2)∵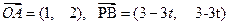 若OABP为平行四边形,
若OABP为平行四边形,
则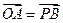
由于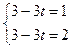 无解,故四边形OABP不能构成平行四边形。
无解,故四边形OABP不能构成平行四边形。
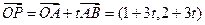 ,若P在x轴上,只需
,若P在x轴上,只需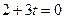 ,∴
,∴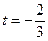 ;
;若P 在y轴上,只需
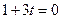 ,∴
,∴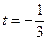 ;
;若P在第二象限,只需
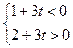 ∴
∴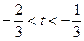
(2)∵
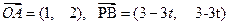 若OABP为平行四边形,
若OABP为平行四边形,则
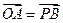
由于
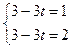 无解,故四边形OABP不能构成平行四边形。
无解,故四边形OABP不能构成平行四边形。
练习册系列答案
相关题目
 ,其中
,其中 三点共线,
三点共线,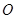 是线外一点,则满足条件的
是线外一点,则满足条件的 ( )
( )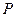 是
是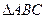 所在平面内一点,
所在平面内一点,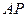 的中点为
的中点为 ,
,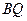 的中点为
的中点为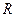 ,
,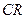 的中点为
的中点为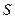 .证明:只有唯一的一点
.证明:只有唯一的一点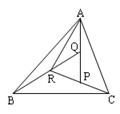
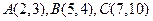 ,若
,若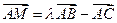 ,试求实数
,试求实数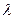 的取值范围,使
的取值范围,使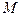 落在第四象限.
落在第四象限. 是AB边上的高,若
是AB边上的高,若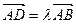 ,则实数λ行等于( )
,则实数λ行等于( )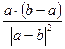 B.
B.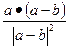 C.
C.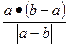 D.
D.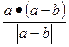
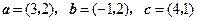 .
.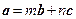 的实数
的实数 ;
; 的实数k;
的实数k;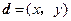 满足
满足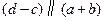 且
且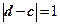 ,求
,求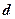 .
. 且
且 ∥
∥ ,则
,则 = ( )
= ( )