题目内容
平面上有相异10个点,每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的
,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为
| 1 | 3 |
3
3
条.分析:设出三点共线直线的条数,分别表示每两点连线可确定的直线的条数、每三点为顶点所确定的三角形个数,利用每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的
,建立方程,即可求得结论.
| 1 |
| 3 |
解答:解:设有x条直线三点共线,则两点连线可以确定直线的条数
-2x,三点为顶点所确定的三角形个数
-x
∵每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的
,
∴
-2x=
(
-x)
∴45-2x=
(120-x)
∴x=3
故答案为:3
| C | 2 10 |
| C | 3 10 |
∵每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的
| 1 |
| 3 |
∴
| C | 2 10 |
| 1 |
| 3 |
| C | 3 10 |
∴45-2x=
| 1 |
| 3 |
∴x=3
故答案为:3
点评:本题考查组合知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
平面上有相异10个点,每两点连线可确定的直线的条数是每三点为顶点所确定的三角形个数的![]() .若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为( )
.若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为( )
A.2条 B.3条
C.4条 D.5条
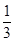 ,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为__________条.
,若无任意四点共线,则这10个点的连线中有且只有三点共线的直线的条数为__________条.