题目内容
已知θ为第四象限角,tan(π+θ)=-2.(1)化简
tan(π-θ)sin(
| ||
| cos(-θ-π)sin(-5π+θ) |
(2)求(1)中式子的值.
分析:(1)根据诱导公式:tan(π-θ)=-tanθ;sin(
-θ)=cosθ;根据余弦函数是偶函数得cos(-θ-π)=cos(π+θ)=-cosθ;根据正弦函数为奇函数得:sin(-5π+θ)=sin(-4π-π+θ)=sin(-π+θ)=-sin(π-θ)=-sinθ,化简原式即可.
(2)根据诱导公式tan(π+θ)=tanθ得到tanθ=-2,然后利用同角三角函数的基本关系及θ的范围得到cosθ的值,代入(1)求出即可.
| π |
| 2 |
(2)根据诱导公式tan(π+θ)=tanθ得到tanθ=-2,然后利用同角三角函数的基本关系及θ的范围得到cosθ的值,代入(1)求出即可.
解答:解:(1)
=
=-
=-
;
(2)∵tan(π+θ)=-2
∴tanθ=
=-2即sinθ=-2cosθ
又sin2θ+cos2θ=1∴cosθ=±
又θ为第四象限角∴cosθ=
∴
=-
=-
.
tan(π-θ)sin(
| ||
| cos(-θ-π)sin(-5π+θ) |
| -tanθcosθ |
| -cosθ(-sinθ) |
=-
| tanθ |
| sinθ |
| 1 |
| cosθ |
(2)∵tan(π+θ)=-2
∴tanθ=
| sinθ |
| cosθ |
又sin2θ+cos2θ=1∴cosθ=±
| ||
| 5 |
又θ为第四象限角∴cosθ=
| ||
| 5 |
∴
tan(π-θ)sin(
| ||
| cos(-θ-π)sin(-5π+θ) |
| 1 |
| cosθ |
| 5 |
点评:考查学生灵活运用诱导公式进行化简求值,灵活运用同角三角函数间的基本关系化简求值.以及运用正弦、余弦函数的奇偶性的性质来解决数学问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
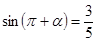 且
且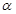 为第四象限角,则
为第四象限角,则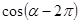 的值是( )
的值是( )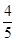 B.
B.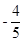 C.
C.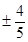 D.
D.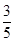
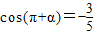 且α为第四象限角,则sin(-2π+α)= .
且α为第四象限角,则sin(-2π+α)= . ,则tanα= .
,则tanα= .