题目内容
已知点(2,2
)在双曲线M:
-
=1(m>0,n>0)上,圆C:(x-a)2+(y-b)2=r2(a>0,b∈R,r>0)与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4.
(Ⅰ)求双曲线M的方程;
(Ⅱ)求圆C的方程;
(Ⅲ)过圆C内一定点Q(s,t)(不同于点C)任作一条直线与圆C相交于点A、B,以A、B为切点分别作圆C的切线PA、PB,求证:点P在定直线l上,并求出直线l的方程.
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
(Ⅰ)求双曲线M的方程;
(Ⅱ)求圆C的方程;
(Ⅲ)过圆C内一定点Q(s,t)(不同于点C)任作一条直线与圆C相交于点A、B,以A、B为切点分别作圆C的切线PA、PB,求证:点P在定直线l上,并求出直线l的方程.
分析:(Ⅰ)由点(2,2
)在双曲线M:
-
=1(m>0,n>0)上,点(1,2)在双曲线M的一条渐近线上,建立方程组,即可求得双曲线M的方程;
(Ⅱ)利用圆C:(x-a)2+(y-b)2=r2(a>0,b∈R,r>0)与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4,建立方程组,即可求得圆C的方程;
(Ⅲ)设A(x1,y1),B(x2,y2),则求出在点A、点B的切线方程,两方程相减,利用Q,A,B三点共线,化简,即可得到结论.
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
(Ⅱ)利用圆C:(x-a)2+(y-b)2=r2(a>0,b∈R,r>0)与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4,建立方程组,即可求得圆C的方程;
(Ⅲ)设A(x1,y1),B(x2,y2),则求出在点A、点B的切线方程,两方程相减,利用Q,A,B三点共线,化简,即可得到结论.
解答:(Ⅰ)解:由题意,点(2,2
)在双曲线M:
-
=1(m>0,n>0)上,点(1,2)在双曲线M的一条渐近线上,则
,∴m=1,n=2,∴双曲线M的方程为x2-
=1;
(Ⅱ)解:∵圆C:(x-a)2+(y-b)2=r2(a>0,b∈R,r>0)与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4
∴
∴a=3,b=1,r=
∴圆C的方程为(x-3)2+(y-1)2=5;
(Ⅲ)证明:设A(x1,y1),B(x2,y2),则在点A的切线方程为(x1-3)(x-3)+(y1-1)(y-1)=5
在点B的切线方程为(x2-3)(x-3)+(y2-1)(y-1)=5
两方程相减可得(x1-x2)(x-3)+(y1-y2)(y-1)=0
∵Q,A,B三点共线
∴(x1-x2)(t-y1)-(y1-y2)(s-x1)=0
∴(x1-s)(x-3)+(y1-t)(y-1)=0
∴(x1-3+3-s)(x-3)+(y1-1+1-t)(y-1)=0
∴(3-s)(x-3)+(1-t)(y-1)+(x1-3)(x-3)+(y1-1)(y-1)=0
∴(s-3)x+(t-1)y-3s-t+5=0
∴点P在定直线l上,直线l的方程为(s-3)x+(t-1)y-3s-t+5=0.
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
|
| y2 |
| 4 |
(Ⅱ)解:∵圆C:(x-a)2+(y-b)2=r2(a>0,b∈R,r>0)与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4
∴
|
∴a=3,b=1,r=
| 5 |
∴圆C的方程为(x-3)2+(y-1)2=5;
(Ⅲ)证明:设A(x1,y1),B(x2,y2),则在点A的切线方程为(x1-3)(x-3)+(y1-1)(y-1)=5
在点B的切线方程为(x2-3)(x-3)+(y2-1)(y-1)=5
两方程相减可得(x1-x2)(x-3)+(y1-y2)(y-1)=0
∵Q,A,B三点共线
∴(x1-x2)(t-y1)-(y1-y2)(s-x1)=0
∴(x1-s)(x-3)+(y1-t)(y-1)=0
∴(x1-3+3-s)(x-3)+(y1-1+1-t)(y-1)=0
∴(3-s)(x-3)+(1-t)(y-1)+(x1-3)(x-3)+(y1-1)(y-1)=0
∴(s-3)x+(t-1)y-3s-t+5=0
∴点P在定直线l上,直线l的方程为(s-3)x+(t-1)y-3s-t+5=0.
点评:本题考查双曲线、圆的方程,考查直线与圆的位置关系,考查直线方程,综合性强,属于中档题.

练习册系列答案
相关题目
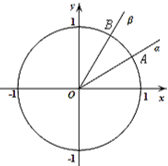 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于AB两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于AB两点.