题目内容
双曲线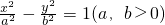 和直线y=2x有交点,则它的离心率的取值范围是________.
和直线y=2x有交点,则它的离心率的取值范围是________.
(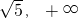 )
)
分析:先计算双曲线的渐近线的方程,过原点的直线y=2x要与双曲线有交点,则其斜率应在(- ,
, )范围内,从而利用a、b、c间的平方关系推出离心率的范围
)范围内,从而利用a、b、c间的平方关系推出离心率的范围
解答:双曲线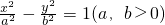 的渐近线方程为y=±
的渐近线方程为y=± x
x
双曲线和直线y=2x有交点,则- <2<
<2<
即4<
即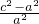 >4
>4
即e2-1>4,
即e2>5,e>
∴双曲线的离心率的取值范围是( ,+∞)
,+∞)
故答案为( ,+∞)
,+∞)
点评:本题考查了双曲线的标准方程及其几何性质,直线与双曲线的位置关系,双曲线渐近线方程及渐近线的作用,离心率的定义及其计算方法
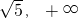 )
)分析:先计算双曲线的渐近线的方程,过原点的直线y=2x要与双曲线有交点,则其斜率应在(-
 ,
, )范围内,从而利用a、b、c间的平方关系推出离心率的范围
)范围内,从而利用a、b、c间的平方关系推出离心率的范围解答:双曲线
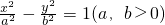 的渐近线方程为y=±
的渐近线方程为y=± x
x双曲线和直线y=2x有交点,则-
 <2<
<2<
即4<

即
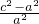 >4
>4即e2-1>4,
即e2>5,e>

∴双曲线的离心率的取值范围是(
 ,+∞)
,+∞)故答案为(
 ,+∞)
,+∞)点评:本题考查了双曲线的标准方程及其几何性质,直线与双曲线的位置关系,双曲线渐近线方程及渐近线的作用,离心率的定义及其计算方法

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
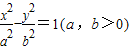 和直线y=2x有交点,则它的离心率的取值范围是 .
和直线y=2x有交点,则它的离心率的取值范围是 .