题目内容
.若过点 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线 的斜率最小值为 ( )
的斜率最小值为 ( )
A. | B. | C. | D. |
B
解析试题分析:因为由曲线 方程可知,该曲线表示的为圆心为(2,0),半径为1的圆,那么根据过点
方程可知,该曲线表示的为圆心为(2,0),半径为1的圆,那么根据过点 的直线
的直线 与曲线
与曲线 有公共点,可知圆心到直线l的距离小于等于圆的半径即可。故设直线l的方程为y=k(x-4),(先考虑斜率不存在不符合题意),那么化为一般式即为kx-y-4k=0,由点到直线的距离公式
有公共点,可知圆心到直线l的距离小于等于圆的半径即可。故设直线l的方程为y=k(x-4),(先考虑斜率不存在不符合题意),那么化为一般式即为kx-y-4k=0,由点到直线的距离公式 ,然后两边平方化简可知
,然后两边平方化简可知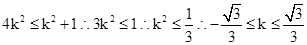 ,可知直线
,可知直线 的斜率最小值为
的斜率最小值为 ,选B.
,选B.
考点:本试题主要是考查了直线与圆的位置关系中相交或者相切的情况的分析和解决。
点评:理解直线与曲线有公共点的含义,就是直线与圆有交点,那么可知直线与圆的位置关系是相交或者相切。

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
圆 和
和 的位置关系为( )
的位置关系为( )
| A.外切 | B.内切 | C.外离 | D.内含 |
圆 和圆
和圆 的位置关系是( )
的位置关系是( )
| A.外切 | B.内切 | C.外离 | D.内含 |
自点A(3,5)作圆C: 的切线,求切线的方程( )
的切线,求切线的方程( )
A. | B. |
C. 或 或 | D.以上都不对 |
已知圆 与抛物线
与抛物线 的准线相切,则
的准线相切,则 的值为()
的值为()
| A.1 | B.2 | C. | D.4 |
从点 向圆C:
向圆C: 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
A. | B.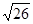 | C. | D.5 |
已知点 (
( )是圆
)是圆 :
: 内一点,直线
内一点,直线 是以
是以 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线 的方程是
的方程是 ,那么
,那么
A. ∥ ∥ 且 且 与圆 与圆 相离 相离 | B.   且 且 与圆 与圆 相离 相离 |
C. ∥ ∥ 且 且 与圆 与圆 相切 相切 | D.   且 且 与圆 与圆 相切 相切 |
 所表示的曲线的图形是( )
所表示的曲线的图形是( )