题目内容
已知增函数 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
.
⑴求函数 的解析式;
的解析式;
⑵求满足 的
的 的范围;
的范围;
(1) ;(2)
;(2)
【解析】
试题分析:(1)由函数 是定义在
是定义在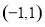 上的奇函数,则有
上的奇函数,则有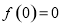 ,可求得
,可求得 ,此时
,此时 ,又有
,又有 ,则有
,则有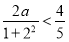 ,即
,即 ,又
,又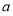 为正整数,所以
为正整数,所以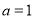 ,从而可求出函数的解析式;(2)由(1)可知
,从而可求出函数的解析式;(2)由(1)可知 ,可知函数
,可知函数 在定义域内为单调递增(可用定义法证明:①在其定义域内任取两个自变量
在定义域内为单调递增(可用定义法证明:①在其定义域内任取两个自变量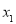 、
、 ,且
,且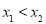 ;②作差(或作商)比较
;②作差(或作商)比较 与
与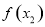 的大小;③得出结论,即若
的大小;③得出结论,即若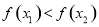 则为单调递增函数,若
则为单调递增函数,若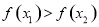 则为单调递减函数),又不等式
则为单调递减函数),又不等式 且
且 为奇函数,所以不等式可化为
为奇函数,所以不等式可化为 ,从而有
,从而有 ,可求出
,可求出 的范围.
的范围.
试题解析:(1)因为 是定义在
是定义在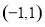 上的奇函数
上的奇函数
所以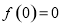 ,解得
,解得 2分
2分
则 ,由
,由 ,得
,得 ,又
,又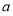 为正整数
为正整数
所以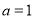 ,故所求函数的解析式为
,故所求函数的解析式为 5分
5分
(2)由(1)可知 且
且 在
在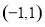 上为单调递增函数
上为单调递增函数
由不等式 ,又函数
,又函数 是定义在
是定义在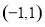 上的奇函数
上的奇函数
所以有 , 8分
, 8分
从而有 10分
10分
解得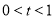 12分
12分
考点:1.函数解析式、奇偶性、单调性;2.不等式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目























