题目内容
已知下列四个命题:①i是虚数单位,则
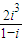 =1-i;
=1-i;②命题“存在x∈R,
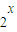 ≤0”的否定是“不存在x∈R,
≤0”的否定是“不存在x∈R,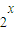 >0”;
>0”;③函数f(x)=ex+x-2在区间(0,1)内有零点;
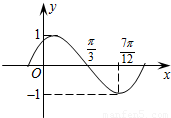
④函数y=sin(ωx+φ)(ω>0,|φ|<
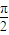 )的图象的一部分如图所示,则ω、φ的值分别为2,-
)的图象的一部分如图所示,则ω、φ的值分别为2,-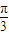 .
.其中是真命题的是( )
A.①②
B.②④
C.③④
D.①③
【答案】分析:①利用复数的四则运算进行化简.②利用特称命题的否定是全称命题去判断.③利用根的存在性定理,验证f(0)f(1)<0是否成立.④根据图象求出对应的ω、φ.
解答:解:①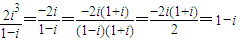 ,所以①正确.
,所以①正确.
②特称命题的否定是全称命题,所以命题“存在x∈R,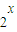 ≤0”的否定是?x∈R,2x>0.所以②错误.
≤0”的否定是?x∈R,2x>0.所以②错误.
③因为函数f(x)=ex+x-2在区间(0,1)上为增函数,且f(0)=2+0-2=-10,
所以根据根的存在定理可知函数f(x)=ex+x-2在区间(0,1)内有零点,所以③正确.
④由图象可知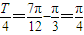 ,解得周期T=π,又
,解得周期T=π,又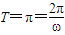 ,所以解得ω=2,此时y=sin(2x+φ).
,所以解得ω=2,此时y=sin(2x+φ).
由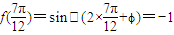 ,解得
,解得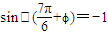 ,
,
即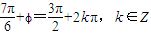 ,解得
,解得 ,
,
因为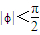 ,所以解得
,所以解得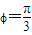 .所以④错误.
.所以④错误.
所以真命题为①③.
故选D.
点评:本题考查各种命题的真假判断,熟练掌握各种命题的判断方法是解决这类问题的关键.
解答:解:①
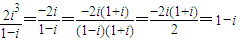 ,所以①正确.
,所以①正确.②特称命题的否定是全称命题,所以命题“存在x∈R,
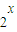 ≤0”的否定是?x∈R,2x>0.所以②错误.
≤0”的否定是?x∈R,2x>0.所以②错误.③因为函数f(x)=ex+x-2在区间(0,1)上为增函数,且f(0)=2+0-2=-10,
所以根据根的存在定理可知函数f(x)=ex+x-2在区间(0,1)内有零点,所以③正确.
④由图象可知
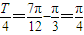 ,解得周期T=π,又
,解得周期T=π,又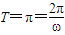 ,所以解得ω=2,此时y=sin(2x+φ).
,所以解得ω=2,此时y=sin(2x+φ).由
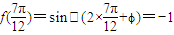 ,解得
,解得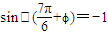 ,
,即
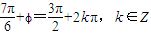 ,解得
,解得 ,
,因为
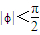 ,所以解得
,所以解得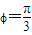 .所以④错误.
.所以④错误.所以真命题为①③.
故选D.
点评:本题考查各种命题的真假判断,熟练掌握各种命题的判断方法是解决这类问题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目