题目内容
如图所示,矩形ABCD的边AB=a,BC=2,PA⊥平面ABCD,PA=2,现有数据:a=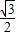 ;a=1;a=2;a=
;a=1;a=2;a=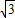 ;a=4.若在BC边上存在点Q,使PQ⊥QD,则a可以取所给数据中的哪些值?并说明理由.
;a=4.若在BC边上存在点Q,使PQ⊥QD,则a可以取所给数据中的哪些值?并说明理由.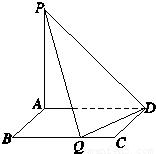
【答案】分析:建立空间直角坐标系,求出各点的坐标,设出点Q的坐标,进而得到向量PQ,QD的坐标,再结合PQ⊥QD即可求出结论.
解答: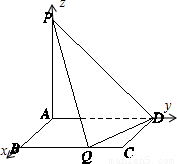 解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)
解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)
设Q(a,x,0)(0≤x≤2),
∵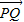 =(a,x,-2),
=(a,x,-2),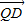 =(-a,2-x,0),
=(-a,2-x,0),
∴由PQ⊥QD得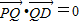 ,
,
∴a2=x(2-x)
∵x∈[0,2],a2=x(2-x)∈(0,1]…
∴在所给数据中,a可取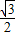 和a=1两个值.
和a=1两个值.
点评:本题考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
解答:
 解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)
解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)设Q(a,x,0)(0≤x≤2),
∵
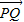 =(a,x,-2),
=(a,x,-2),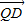 =(-a,2-x,0),
=(-a,2-x,0),∴由PQ⊥QD得
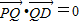 ,
,∴a2=x(2-x)
∵x∈[0,2],a2=x(2-x)∈(0,1]…
∴在所给数据中,a可取
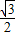 和a=1两个值.
和a=1两个值.点评:本题考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
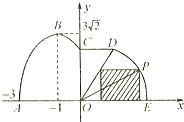 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为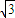 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时