题目内容
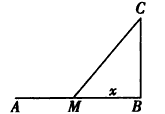
 如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?分析:由已知,我们可计算出公路上的运费和铁路上的运费,进而得到由A到C的总运费,
利用导数法,我们可以分析出函数的单调性,及函数的最小值点,得到答案.
利用导数法,我们可以分析出函数的单调性,及函数的最小值点,得到答案.
解答:解:设M为AB上的一点,且MB=x,于是AM上的运费为2(50-x),MC上的运费为4
,
则由A到C的总运费为
p(x)=2(50-x)+4
(0≤x≤50).
p′(x)=-2+
,
令p′(x)=0,解得x1=
,x2=-
(舍去).
当x<
时,p′(x)<0;当x>
时,p′(x)>0,
故当x=
时,p(x)取得最小值.
即在离点B距离为
的点M处修筑公路至C时,货物运费最省.
| 102+x2 |
则由A到C的总运费为
p(x)=2(50-x)+4
| 100+x2 |
p′(x)=-2+
| 4x | ||
|
令p′(x)=0,解得x1=
| 10 | ||
|
| 10 | ||
|
当x<
| 10 | ||
|
| 10 | ||
|
故当x=
| 10 | ||
|
即在离点B距离为
10
| ||
| 3 |
点评:本题考查的知识点是导数在最大值最小值问题中的应用,函数最值的应用,其中根据已知条件求出函数的解析式,并确定函数的单调性是解答本题的关键.

练习册系列答案
相关题目