题目内容
设椭圆![]() 的左焦点为F1(-2,0),直线
的左焦点为F1(-2,0),直线![]() 与x轴交与点N(-3,0),过点N且倾斜角为30°的直线
与x轴交与点N(-3,0),过点N且倾斜角为30°的直线![]() 交椭圆于A,B两点.
交椭圆于A,B两点.
(1)求直线![]() 和椭圆的方程;
和椭圆的方程;
(2)求证:点![]() 在以线段AB为直径的圆上;
在以线段AB为直径的圆上;
(3)在直线![]() 上有两个不重合的动点C,D,以CD为直径且过点F1的所有圆中,求面积最小的圆的半径长。
上有两个不重合的动点C,D,以CD为直径且过点F1的所有圆中,求面积最小的圆的半径长。
解:(1)可知直线![]() ,由c=2,
,由c=2,![]() ,解得
,解得![]() ,
,
所以![]() 椭圆的方程为:
椭圆的方程为:![]()
(2)联立方程组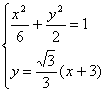 整理得,
整理得,![]() ,
,
设![]() ,则
,则![]() ,
,
因为F1(-2,0),所以,![]()
![]()
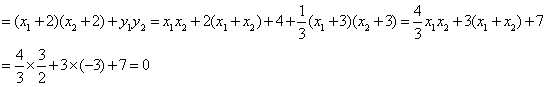 所以点
所以点![]() 在以线段AB为直径的圆上.
在以线段AB为直径的圆上.
(3)面积最小的圆的半径长应是点F1 到直线![]() 的距离.
的距离.
设为d=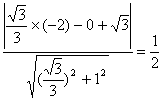

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆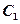 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. 过点F1,且垂直于椭圆的长轴,动直线
过点F1,且垂直于椭圆的长轴,动直线 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. 过点F1,且垂直于椭圆的长轴,动直线
过点F1,且垂直于椭圆的长轴,动直线 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直 垂直
垂直 的离心率为
的离心率为 ,
, 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直 垂直
垂直