题目内容
(本题8分)已知直线l1:2x-y+2=0与l2:x+2y-4=0,点P(1, m).
(Ⅰ)若点P到直线l1, l2的距离相等,求实数m的值;
(Ⅱ)当m=1时,已知直线l经过点P且分别与l1, l2相交于A, B两点,若P恰好
平分线段AB,求A, B两点的坐标及直线l的方程.
【答案】
(Ⅰ)m=-1或m=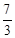 ;
(Ⅱ)x+7y-8=0。
;
(Ⅱ)x+7y-8=0。
【解析】(I)根据点到直线的距离公式建立关于m的方程,求出m的值.
(II)设A(a, 2a+2), B(4-2b, b),因为P(1,1)为AB的中点,根据中点坐标公式可得关于a,b的方程,解出a,b的值.所以可得A、B的坐标,进而得到直线l的方程.
(Ⅰ)由题意得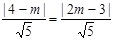 ,…………………………………1分
,…………………………………1分
解得m=-1或m=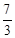 ;………………………………………………2分
;………………………………………………2分
(Ⅱ)设A(a, 2a+2), B(4-2b, b),则
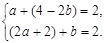 解得
解得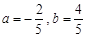 ,………………………………2分
,………………………………2分
∴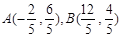 ,∴
,∴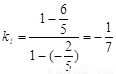 ,……………………2分
,……………………2分
∴l: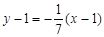 ,即x+7y-8=0………………………………1分
,即x+7y-8=0………………………………1分

练习册系列答案
相关题目
 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.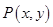 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线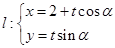 (
( 为参数),圆
为参数),圆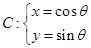 (
(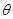 为参数).
为参数). 时,试判断直线
时,试判断直线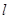 与圆
与圆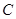 的位置关系;
的位置关系;