Question

函数y=sinx和y=cosx的图象在[0，8π]内的所有交点中，能确定的不同直线的条数是

1. A.
   28
2. B.
   18
3. C.
   16
4. D.
   6

Answer 1

B
分析：在一个坐标系画出函数y=sinx、y=cosx在[0，2π]的图象，由图得在一个周期内的交点个数，故得到在[0，8π]内的所有交点个数，根据交点的位置，判断重合的直线条数，再确定的不同直线的条数．
解答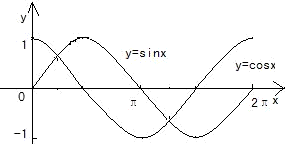：解：在一个坐标系画出函数y=sinx、y=cosx在[0，2π]的图象：
由图得，两函数在一个周期上的交点个数是2个，
则在区间[0，8π]内交点的个数应是8个，
有因由x轴上方四个点共线，下方的四个点也共线，
则8个交点中能确定的不同直线的条数是C₈²-2C₄²+2=18．
故选B．
点评：本题的考点是正弦（余弦）函数的图象，即根据一个周期内的图象特点得出在区间上的特点，此题注意直线重合的情况．