题目内容
从一个箱子中，一同学从4个不同黑球和2个不同白球共6个球中任取3个球，则所选的球中既有白球又有黑球的概率为
- A.
- B.
- C.
- D.
D
分析：从6个球中任取3个球共有
=20种取法，而符合条件的共有有
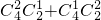=16种取法，由古典概型的概率公式可得．
解答：从6个球中任取3个球共有=20种取法，
而所选的球中既有白球又有黑球是指：2个黑球1个白球，或1个黑球2个白球，
共有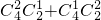=16种取法，
故所求事件的概率为：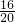
=
故选D
点评：本题为古典概型的求解，涉及排列组合的知识，属基础题．
分析：从6个球中任取3个球共有
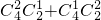=20种取法，而符合条件的共有有=16种取法，由古典概型的概率公式可得．解答：从6个球中任取3个球共有
=20种取法，而所选的球中既有白球又有黑球是指：2个黑球1个白球，或1个黑球2个白球，
共有
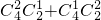=16种取法，故所求事件的概率为：
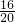=故选D
点评：本题为古典概型的求解，涉及排列组合的知识，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
