题目内容
在[-π，π]内，函数y=sin(x-| π | 3 |
分析：由不等式2kπ-
≤x-
≤2kπ+
，求出x的取值范围，即得到函数y=sin(x-
)为增函数的区间．
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
解答：解：由函数y=sin(x-
) 的解析式得，增区间满足 2kπ-
≤x-
≤2kπ+
，
∴2kπ-
≤x≤2kπ+
，k∈z，又x∈[-π，π]，
∴-
≤x≤
，故增区间为[-
，
]，
故答案为[-
，
]．
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴2kπ-
| π |
| 6 |
| 5π |
| 6 |
∴-
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
故答案为[-
| π |
| 6 |
| 5π |
| 6 |
点评：本题考查正弦函数的增区间的求法，列出不等式 2kπ-
≤x-
≤2kπ+
，是解题的关键．
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
]内，则输入的实数x的取值范围是（ ）
，
]
，
]
，
]
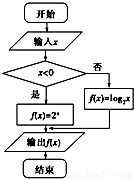
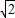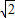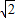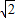]内，则输入的实数x的取值范围是（ ）
，
]
，
]
，
]
]内，则输入的实数x的取值范围是（ ）
，
]
，
]
，
]
]内，则输入的实数x的取值范围是（ ）
，
]
，
]
，
]
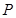（元）与时间
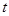（天）的函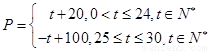
，该商品的日销售量Q(件)与时间t（天）
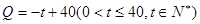，求这种商品日销售金额的最大值，