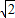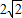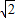Question

直线y=x截圆（x-2）²+y²=4所得的弦长为（　　）

• A、1
• B、2

  2

• C、2
• D、

  2

Answer 1

分析：由已知中直线y=x和圆（x-2）²+y²=4的方程，求出圆心坐标和半径，及弦心距，根据半弦长，弦心距，圆半径构成直角三角形，满足勾股定理，求出弦长．

解答：解：圆（x-2）²+y²=4的圆心为（2，0），半径R=2
则圆心到直线y=x的距离d=

2

由半弦长，弦心距，圆半径构成直角三角形，满足勾股定理
可得l=2

R2-d2

=2

2

故选B

点评：本题考查的知识点是直线和圆的方程的应用，其中根据半弦长，弦心距，圆半径构成直角三角形，满足勾股定理，是求直线截圆所得弦长最常用的方法．