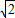Question

点M，N在圆x²+y²+kx+2y-4=0上，且点M，N关于直线l：x-y+1=0对称，则该圆的半径为（　　）

• A．2

  2

• B．

  2

• C．3
• D．1

Answer 1

分析：圆上的点关于直线对称，则直线经过圆心，求出圆的圆心，代入直线方程，即可求出k，然后求出半径．

解答：解：圆x²+y²+kx+2y-4=0的圆心坐标为（-

k

2

，-1），
因为点M，N在圆x²+y²+kx+2y-4=0上，且点M，N关于直线l：x-y+1=0对称，
所以直线l：x-y+1=0经过圆心，
所以-

k

2

+1+1=0，k=4．
所以圆的方程为：x²+y²+3x+2y-4=0，圆的半径为：

1

2

42+22-4×(-4)

=3．
故选C．

点评：本题考查直线与圆的位置关系，考查圆的一般方程的应用，考查计算能力．