题目内容
下列命题:
①若m∈(0,1],则m+
≥2
;
②
=-1;
③若无穷数列an=
,其各项和S=
;
④log32>ln2>
;
⑤设f(x)=
,(x≠1),f'(x)为其导函数,若f'(a)=f'(b),(a≠b),则f(a)+f(b)=4.
其中正确命题有
①若m∈(0,1],则m+
| 3 |
| m |
| 3 |
②
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
③若无穷数列an=
| 1 |
| n(n+2) |
| 3 |
| 4 |
④log32>ln2>
| 1 |
| 2 |
⑤设f(x)=
| 2x+1 |
| x-1 |
其中正确命题有
②③⑤
②③⑤
.(请填上你认为正确的所有命题的序号,多填少填均不得分)分析:①若m∈(0,1],则m+
≥2
,当且仅当m=
,即m=
时,取等号,因为
∉(0,1],知①不正确;②
=
=-1;③若无穷数列an=
=
(
-
),由Sn=a1+a2+…+an=
-
•
,由此知其各项和S=
Sn=
(
-
•
)=
;④由3>e,知log32<ln2;⑤设f(x)=
,(x≠1),f'(x)为其导函数,若f'(a)=f'(b),(a≠b),则f(a)+f(b)=4.
| 3 |
| m |
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
| 2x+1 |
| x-1 |
解答:解:①若m∈(0,1],则m+
≥2
,
当且仅当m=
,即m=
时,取等号,
因为
∉(0,1],故①不正确;
②
=
=-1,故②正确;
③若无穷数列an=
=
(
-
),
则Sn=a1+a2+…+an
=
(1-
)+
(
-
)+
(
-
)+…+
(
-
)
=
(
-
-
)=
-
•
,
∴其各项和S=
Sn=
(
-
•
)=
,故③正确.
④∵3>e,∴log32<ln2,故④不正确;
⑤设f(x)=
,(x≠1),f'(x)为其导函数,
若f'(a)=f'(b),(a≠b),则f(a)+f(b)=4,故⑤正确.
故答案为:②③⑤.
| 3 |
| m |
| 3 |
当且仅当m=
| 3 |
| m |
| 3 |
因为
| 3 |
②
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
③若无穷数列an=
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
则Sn=a1+a2+…+an
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
∴其各项和S=
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
④∵3>e,∴log32<ln2,故④不正确;
⑤设f(x)=
| 2x+1 |
| x-1 |
若f'(a)=f'(b),(a≠b),则f(a)+f(b)=4,故⑤正确.
故答案为:②③⑤.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,注意均值定理、数列的极限、对数函数、导数等知识点的灵活运用.

练习册系列答案
相关题目
已知
m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:(1)
若m∥β,n∥β且m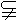 α,n
α,n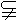 α,则α∥β;
α,则α∥β;
(2)
若α∩β=n,m∥n,则m∥α且m∥β;(3)
若m⊥α,m∥β,则α⊥β;(4)
若α∥β,且γ∩α=m,γ∩β=n,则m∥n.其中的正确命题是
[
]|
A .(1)和(3) |
B .(1)和(4) |
|
C .(2)和(4) |
D .(3)和(4) |
 α,n
α,n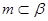 ,则α⊥β
,则α⊥β