题目内容
如图2-3-24,AB,CD为圆的两条相交弦,且不全为直径.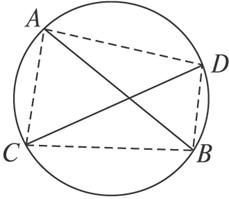
图2-3-24
求证:AB,CD不能互相平分.
证明:假设AB,CD互相平分,则ACBD为平行四边形,
所以∠ACB=∠ADB,∠CAD=∠CBD.
因为ABCD为圆内接四边形,
所以∠ACB+∠ADB=180°,∠CAD+∠CBD=180°.
因此∠ACB=90°,∠CAD=90°.
所以,对角线AB,CD均为直径,与已知矛盾,因此,AB,CD不能互相平分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
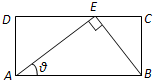 某学校需要一批一个锐角为θ的直角三角形硬纸板作为教学用具(
某学校需要一批一个锐角为θ的直角三角形硬纸板作为教学用具(


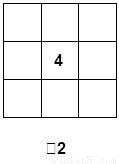
 数字1,2,3,…,9这九条数字填写在如图2所示的9个空格中,要求每一行从左到右依次增大,每一列从上到下也依次增大,当中心位置填上4后,所有填写空格的方法共有
数字1,2,3,…,9这九条数字填写在如图2所示的9个空格中,要求每一行从左到右依次增大,每一列从上到下也依次增大,当中心位置填上4后,所有填写空格的方法共有