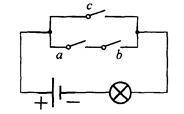
题目内容
用A、B、C三类不同的元件连接成两个系统N1、N2当元件A、B、C都正常工作时,系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作。已知元件A、B、C正常工作的概率依次为0.80, 0.90, 0.90,分别求系统N1、N2正常工作的概率.
 | |
 |
0.792
解:分别记三个元件A、B、C能正常工作为事件A、B、C,由题意,这三个事件
相互独立,系统N1正常工作的概率为
P(A·B·C)=P(A)·P(B)·P(C)= 0.8´0.9´0.9 = 0.648
系统N2中,记事件D为B、C至少有一个正常工作,则
P(D)=1–P(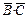 )="1–" P(
)="1–" P(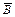 )·P(
)·P(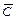 )=1–(1 –0.9)´(1–0.9)= 0.99
)=1–(1 –0.9)´(1–0.9)= 0.99
系统N2正常工作的概率为P(A·D)= P(A)·P(D)= 0.8´0.99 = 0.792。
相互独立,系统N1正常工作的概率为
P(A·B·C)=P(A)·P(B)·P(C)= 0.8´0.9´0.9 = 0.648
系统N2中,记事件D为B、C至少有一个正常工作,则
P(D)=1–P(
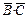 )="1–" P(
)="1–" P(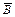 )·P(
)·P(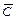 )=1–(1 –0.9)´(1–0.9)= 0.99
)=1–(1 –0.9)´(1–0.9)= 0.99系统N2正常工作的概率为P(A·D)= P(A)·P(D)= 0.8´0.99 = 0.792。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,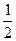 ,
,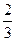 ,对于该大街上行驶的汽车,求:
,对于该大街上行驶的汽车,求: ,则
,则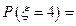 .
.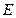 与
与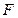 相互独立,且
相互独立,且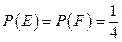 ,则
,则 的值等于
的值等于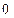
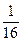
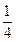

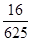
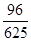
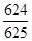
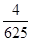

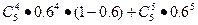
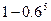
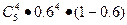
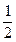 ,且是相互独立的,求灯亮的概率.
,且是相互独立的,求灯亮的概率.