Question

设等比数列的公比为q，前n项和为S­_n，若S_n+1,S­_n，S_n+2成等差数列，则q的值为  

 

Answer 1

【答案】

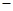2

【解析】

试题分析：设等比数列{a_n}的公比为q，前n项和为S_n，且S_n+1，S_n，S_n+2成等差数列，则2S_n=S_n+1+S_n+2 ．

若q=1，则S_n=na₁，式显然不成立．

若q≠1，则

=+

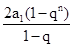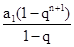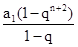
故2qⁿ=qⁿ⁺¹+qⁿ⁺²，即q²+q-2=0，因此q=-2．

考点：本题主要考查等差数列的定义和性质，等比数列的前n项和公式。

点评：涉及等比数列求和时，若公比为字母，则需要分类讨论，属中档题．