题目内容
如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米, .若游客在每条路线上游览的“心悦效果”均与相应的线段或弧的长度成正比,且中间路线DE,DF,EF的比例系数为2k,两边路线DA,DB,AE,BF的比例系数为k(k>0),假定该公园整体的“心悦效果”y是游客游览所有路线“心悦效果”的和.
.若游客在每条路线上游览的“心悦效果”均与相应的线段或弧的长度成正比,且中间路线DE,DF,EF的比例系数为2k,两边路线DA,DB,AE,BF的比例系数为k(k>0),假定该公园整体的“心悦效果”y是游客游览所有路线“心悦效果”的和.(1)试将y表示为x的函数;
(2)试确定当x取何值时,该公园整体的“心悦效果”最佳?
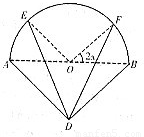
【答案】分析:(1)由题意知,建立三角函数模型,根据所给的条件看出要用的三角形的边长和角度,用余弦定理写出要求的边长,表述出函数式,整理变化成最简的形式,得到结果.
(2)要求函数的单调性,对上一问整理的函数式求导,利用导数求出函数的单增区间和单减区间,看出变量x取到的结果.
解答:解:(1)∵∠EOA=∠FOB=2x,
∴弧EF、AE、BF的长分别为π-4x,2x,2x
连接OD,则由OD=OE=OF=1,
∠FOD=∠EOD=2x+ ,
,
∴DE=DF= =
= =
= (sinx+cosx),
(sinx+cosx),
∴y=2k[2 (sinx+cosx)+π-4x]+k(2
(sinx+cosx)+π-4x]+k(2 +4x)=2k[2
+4x)=2k[2 (sinx+cosx)-2x+
(sinx+cosx)-2x+ +π];
+π];
(2)∵由y′=4k[ (sinx+cosx)-1]=0,
(sinx+cosx)-1]=0,
解得:cos(x+ )=
)= ,即x=
,即x= ,
,
又当x∈(0, )时,y'>0,此时y在(0,
)时,y'>0,此时y在(0, )上单调递增;
)上单调递增;
当x∈( ,
, ))时,y'<0,此时y在(
))时,y'<0,此时y在( ,
, )上单调递减.
)上单调递减.
故当x= 时,该公园整体的“心悦效果”最佳.
时,该公园整体的“心悦效果”最佳.
点评:本题是一道难度较大的题,表现在以下几个方面第一需要自己根据条件建立三角函数模型写出解析式,再对解析式进行整理运算,得到函数性质,这是一个综合题,解题的关键是读懂题意.
(2)要求函数的单调性,对上一问整理的函数式求导,利用导数求出函数的单增区间和单减区间,看出变量x取到的结果.
解答:解:(1)∵∠EOA=∠FOB=2x,
∴弧EF、AE、BF的长分别为π-4x,2x,2x
连接OD,则由OD=OE=OF=1,
∠FOD=∠EOD=2x+
 ,
,∴DE=DF=
 =
= =
= (sinx+cosx),
(sinx+cosx),∴y=2k[2
 (sinx+cosx)+π-4x]+k(2
(sinx+cosx)+π-4x]+k(2 +4x)=2k[2
+4x)=2k[2 (sinx+cosx)-2x+
(sinx+cosx)-2x+ +π];
+π];(2)∵由y′=4k[
 (sinx+cosx)-1]=0,
(sinx+cosx)-1]=0,解得:cos(x+
 )=
)= ,即x=
,即x= ,
,又当x∈(0,
 )时,y'>0,此时y在(0,
)时,y'>0,此时y在(0, )上单调递增;
)上单调递增;当x∈(
 ,
, ))时,y'<0,此时y在(
))时,y'<0,此时y在( ,
, )上单调递减.
)上单调递减.故当x=
 时,该公园整体的“心悦效果”最佳.
时,该公园整体的“心悦效果”最佳.点评:本题是一道难度较大的题,表现在以下几个方面第一需要自己根据条件建立三角函数模型写出解析式,再对解析式进行整理运算,得到函数性质,这是一个综合题,解题的关键是读懂题意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
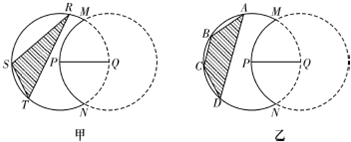
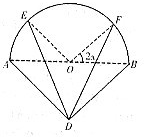 如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,
如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米, (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积. (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.