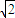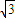题目内容
已知点M，N是曲线y=sinπx与曲线y=cosπx的两个不同的交点，则|MN|的最小值为（ ）
分析：|MN|的最小值即一个周期内两个交点的距离，列出方程求出两个交点坐标，据两点的距离公式求出|MN|的最小值．
解答：解：要求|MN|的最小值在，只要在一个周期内解即可．
∵sinπx=cosπx，解得πx=
或
，即x=
或
．
故可以令点M，N的坐标分别为（
，
）或（
，-
），
故|MN|=
=
，故|MN|的最小值为
，
故选C．
∵sinπx=cosπx，解得πx=
| π |
| 4 |
| 5π |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
故可以令点M，N的坐标分别为（
| 1 |
| 4 |
| ||
| 2 |
| 5 |
| 4 |
| ||
| 2 |
故|MN|=
(
|
| 3 |
| 3 |
故选C．
点评：本题考查等价转化的数学思想方法、两点的距离公式的应用，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
